题目内容
设A在x轴上,它到点P(0,
,3)的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是( )
| 2 |
| A、(1,0,0)和(-1,0,0) | ||||||||
| B、(2,0,0)和(-2,0,0) | ||||||||
C、(
| ||||||||
D、(-
|
分析:根据A在x轴上,设A点的坐标是(x,0,0),根据A到点P(0,
,3)的距离等于到点Q(0,1,-1)的距离的两倍,写出关于x的关系式,求出点的坐标.
| 2 |
解答:解:∵A在x轴上,
∴设A点的坐标是(x,0,0)
∵A到点P(0,
,3)的距离等于到点Q(0,1,-1)的距离的两倍,
∴|AP|=2|AQ|
∴
=2
∴x=±1,
故选A.
∴设A点的坐标是(x,0,0)
∵A到点P(0,
| 2 |
∴|AP|=2|AQ|
∴
| x2+2+9 |
| x2+1+1 |
∴x=±1,
故选A.
点评:本题考查空间中点的坐标和两点之间的距离,本题解题的关键是根据点的位置,设出点的坐标,设出简单的坐标形式是解题的捷径.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
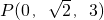 的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是
的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是 ,0,0)和(
,0,0)和( ,0,0)
,0,0) ,0,0)和(
,0,0)和( ,0,0)
,0,0) 的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是( )
的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是( ) ,0,0)和(
,0,0)和(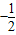 ,0,0)
,0,0)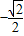 ,0,0)和(
,0,0)和(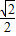 ,0,0)
,0,0) 的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是( )
的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是( ) ,0,0)和(
,0,0)和( ,0,0)
,0,0) ,0,0)和(
,0,0)和(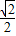 ,0,0)
,0,0)