题目内容
已知抛物线的顶点在坐标原点,焦点在 轴上,且过点
轴上,且过点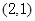 .
.
(1)求抛物线的标准方程;
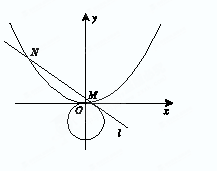
(2)与圆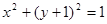 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 若抛物线上一点
若抛物线上一点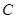 满足
满足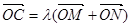
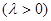 ,求
,求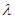 的取值范围.
的取值范围.
(1)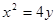 ;(2)
;(2)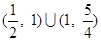 .
.
解析试题分析:(1)设出抛物线方程,求出p,得到标准方程;(2)把直线方程代入抛物线方程,得到一元二次方程,根据韦达定理得到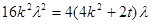 ,转化得到
,转化得到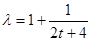 ,根据
,根据 或
或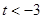 求出
求出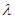 的取值范围为
的取值范围为 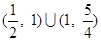 .
.
试题解析:(1) 设抛物线方程为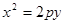 ,
,
由已知得: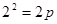 所以
所以 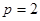
所以抛物线的标准方程为 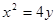
(2) 因为直线与圆相切,
所以 
把直线方程代入抛物线方程并整理得: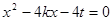
由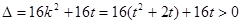
得  或
或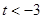
设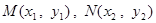 ,
,
则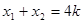

由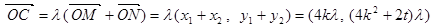
得 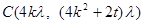
因为点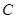 在抛物线
在抛物线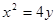 上,
上,
所以,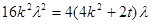
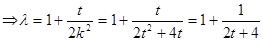
因为 或
或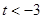 ,
,
所以 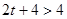 或
或 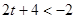
所以 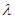 的取值范围为
的取值范围为 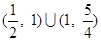 .
.
考点:抛物线标准方程,联立法解直线与抛物线位置关系问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 中,已知椭圆
中,已知椭圆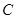 :
: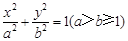 的离心率
的离心率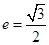 ,且椭圆C上一点
,且椭圆C上一点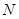 到点Q
到点Q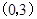 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆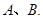
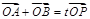 (O为坐标原点),当
(O为坐标原点),当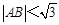 时,求实数
时,求实数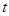 的取值范围.
的取值范围.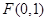 且与直线
且与直线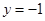 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为 .点
.点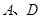 在轨迹
在轨迹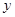 轴对称,过线段
轴对称,过线段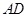 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线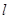 ,使直线
,使直线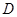 处的切线平行,设直线
处的切线平行,设直线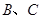 .
.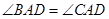 ;
;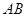 的距离等于
的距离等于 ,且
,且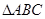 的面积为20,求直线
的面积为20,求直线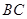 的方程.
的方程.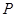 :
: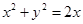 及抛物线
及抛物线 :
: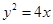 ,过圆心
,过圆心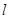 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为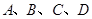 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线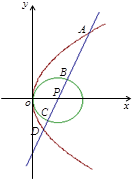
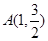 ,两个焦点为
,两个焦点为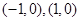 .
.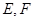 是椭圆C上的两个动点,如果直线
是椭圆C上的两个动点,如果直线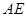 的斜率与
的斜率与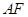 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线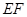 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.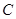 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为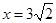 ,离心率为
,离心率为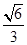 .若直线
.若直线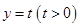 与椭圆
与椭圆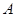 、
、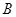 ,以线段
,以线段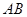 为直径作圆
为直径作圆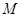 .
.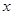 轴相切,求圆
轴相切,求圆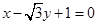 截得的线段长.
截得的线段长.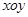 中,已知
中,已知 ,
,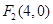 ,
,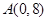 ,直线
,直线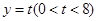 与线段
与线段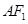 、
、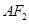 分别交于点
分别交于点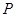 、
、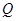 .
.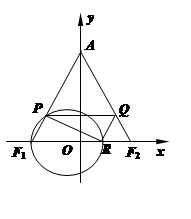
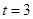 时,求以
时,求以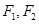 为焦点,且过
为焦点,且过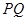 中点的椭圆的标准方程;
中点的椭圆的标准方程;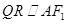 交
交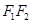 于点
于点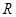 ,记
,记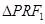 的外接圆为圆
的外接圆为圆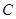 .
.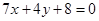 上;
上;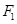 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由. 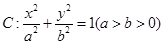 的离心率为
的离心率为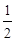 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线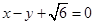 相切,直线
相切,直线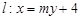 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.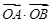 的取值范围;
的取值范围;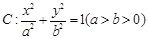 的离心率为
的离心率为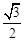 ,且经过点
,且经过点 .
.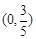 的直线与椭圆交于
的直线与椭圆交于 两点(
两点(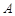 点不重合),
点不重合),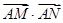 的值;
的值;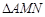 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线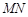 的方程.
的方程.