Question

【题目】尧盛机械生产厂每生产某产品（百台），其总成本为（万元），其中固定成本为万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）．销售收入（万元）满足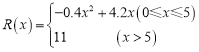，假定生产的产品都能卖掉，请完成下列问题：

（1）写出利润函数的解析式（注：利润=销售收入-总成本）；

（2）试问该工厂生产多少台产品时，可使盈利最多?

Answer 1

【答案】（1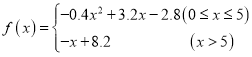）；（2）生产4百台时，利润最大。

【解析】

试题分析：（1）设生产机械百台机械，此时固定成本为2.8万元，生产成本为万元，此时总成本为万元，由于销售收入满足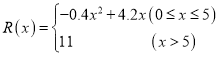，根据利润=销售收入-总成本，所以利润函数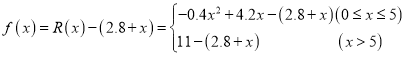；（2）本问实际上是求利润函数的最大值，当时，在区间上递增，在区间上递减，所以当时，取得最大值，，当时，在区间单调递减，所以，因此可知，当工厂生产4百台产品时，利润最大。

试题解析：（1）由题意得

∴．

（2）当时，∵函数递减，∴<=（万元）．

当时，函数

当时，有最大值为（万元）

∴当工厂生产400台时，可使赢利最大为万元．