题目内容
用反证法证明:如果 ,那么
,那么 。
。
 ,那么
,那么 。
。如下
试题分析:证明:假设
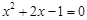 ,则
,则
容易看出
 ,下面证明
,下面证明 .
. 要证明:
 成立,
成立,只需证:
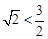 成立,
成立, 只需证:
 成立,
成立,上式显然成立,故有
 成立.
成立. 综上,
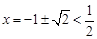 ,与已知条件
,与已知条件 矛盾.
矛盾.因此,
 .
. 点评:反证法是从要证明的结论的反面入手,当否定了反面,正面就能成立。当问题从正面无法解决时,常用反证法。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,  ,
,  ,
, ,
, 按上述规律展开后,发现等式右边含有“
按上述规律展开后,发现等式右边含有“ ”这个数,则
”这个数,则 _______.
_______.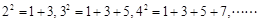
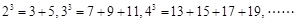
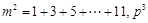 的分解中最小的正整数是21,则
的分解中最小的正整数是21,则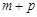 =( )
=( ) 是减函数(大前提),而y=
是减函数(大前提),而y= 是对数函数(小前提),所以y=
是对数函数(小前提),所以y=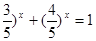 ”有如下思路;设
”有如下思路;设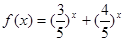 ,则
,则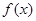 在R上单调递减,且
在R上单调递减,且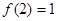 ,故原方程有唯一解x=2,类比上述解题思路,不等式
,故原方程有唯一解x=2,类比上述解题思路,不等式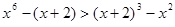 的解集是 .
的解集是 .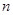 为正整数,
为正整数,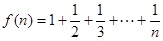 ,计算得
,计算得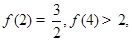
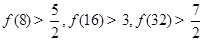 ,观察上述结果,可推测出一般结论( )
,观察上述结果,可推测出一般结论( )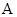 .
.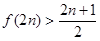 ;
;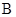 .
.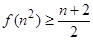 ;
; 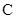 .
. 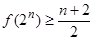 ;
;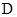 .以上都不对
.以上都不对 五个方面的多元评价指标,并通过经验公式
五个方面的多元评价指标,并通过经验公式 来计算各班的综合得分,
来计算各班的综合得分, 的值越高则评价效果越好.若某班在自测过程中各项指标显示出
的值越高则评价效果越好.若某班在自测过程中各项指标显示出 ,则下阶段要把其中一个指标的值增加
,则下阶段要把其中一个指标的值增加 个单位,而使得
个单位,而使得