Question

【题目】已知点P（ ， ）在椭圆E： + =1（a＞b＞0）上，F为右焦点，PF垂直于x轴，A，B，C，D为椭圆上四个动点，且AC，BD交于原点O．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设A（x1 ， y1），B（x2 ， y2），满足 = ，判断kAB+kBC的值是否为定值，若是，求出此定值，并求出四边形ABCD面积的最大值，否则请说明理由．

Answer 1

【答案】解：（Ⅰ）由题意可知：PF垂直于x轴，则c= ， = ，即a=2b2 ，
a2﹣b2=c2=3，
则a=2，b=1，
∴椭圆的标准方程： ；
（Ⅱ）∵ = ，4y1y2=x1x2 ，
若直线AB的斜率不存在（或AB的斜率为0时），不满足4y1y2=x1x2；
直线AB的斜率存在且不为0时，设直线方程为y=kx+m，A（x1 ， y1），B（x2 ， y2）．
联立 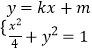，得（1+4k2）x2+8kmx+4（m2﹣1）=0．
△=（8km）2﹣4（1+4k2）（4m2﹣4）=16（4k2﹣m2+1）＞0，①
x1+x2=﹣ ，x1x2= ．
∵4y1y2=x1x2 ， 又y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2 ，
∴（4k2﹣1）x1x2+4km（x1+x2）+4m2=0，
即（4k2﹣1） +4km（﹣ ）+4m2=0．
整理得：k=± ．
∵A、B、C、D的位置可以轮换，
∴AB、BC的斜率一个是 ，另一个就是﹣ ．
∴kAB+kBC= ﹣ =0，是定值．
不妨设kAB=﹣ ，则x1+x2=2m，x1x2=2（m2﹣1）．
设原点到直线AB的距离为d，则S△AOB= |AB|d= |x1﹣x2|
= = ≤1．
当m2=1时满足①取等号．
∴S四边形ABCD=4S△AOB≤4，即四边形ABCD面积的最大值为4．
∴四边形ABCD面积的最大值为4．
【解析】（Ⅰ）由题意可知a=2b2 ， a2﹣b2=c2=3，即可求得a和b的值，求得椭圆方程；（Ⅱ）由4y1y2=x1x2 ， 当直线AB的斜率存在且不为0时，设直线方程为y=kx+m，代入椭圆方程，利用根与系数的关系求得A，B的横坐标的和与积，结合4y1y2=x1x2 ， 求得k，把三角形AOB的面积化为关于m的函数，利用基本不等式求其最值，进一步得到四边形ABCD面积的最大值．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．