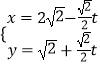题目内容
【题目】一种画椭圆的工具如图1所示．O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3，当栓子D在滑槽AB内作往复运动时，带动N绕O转动，M处的笔尖画出的椭圆记为C，以O为原点，AB所在的直线为x轴建立如图2所示的平面直角坐标系．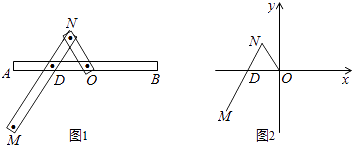 
（1）求椭圆C的方程；
（2）设动直线l与两定直线l1：x﹣2y=0和l2：x+2y=0分别交于P，Q两点．若直线l总与椭圆C有且只有一个公共点，试探究：△OPQ的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．
【答案】
（1）解：设D（t，0），|t|≤2，
N（x0，y0），M（x，y），由题意得 
=2 
，
且| |=| 
|=1，
∴（t﹣x，﹣y）=2（x0﹣t，y0），且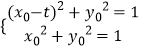 
，
即 
，且t（t﹣2x0）=0，
由于当点D不动时，点N也不动，∴t不恒等于0，
于是t=2x0，故x0= 
，y0=﹣ 
，
代入x02+y02=1，得方程为 
．
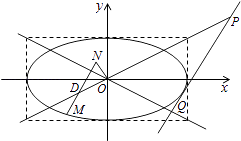
（2）解：①当直线l的斜率k不存在时，直线l为：x=4或x=﹣4，都有S△OPQ= 
，
②直线l的斜率k存在时，直线l为：y=kx+m，（k 
），
由 
消去y，可得（1+4k2）x2+8kmx+4m2﹣16=0，
∵直线l总与椭圆C有且只有一个公共点，
∴△=64k2m2﹣4（1+4k2）（4m2﹣16）=0，即m2=16k2+4，①，
由 
，可得P（ 
， 
），同理得Q（ 
， 
），
原点O到直线PQ的距离d= 
和|PQ|= 
|xP﹣xQ|，
可得S△OPQ= 
|PQ|d= |m||xP﹣xQ|= |m|| 
|=| 
|②，
将①代入②得S△OPQ=| |=8| 
|，
当k2＞ 
时，S△OPQ=8（ ）=8（1+ 
）＞8，
当0≤k2＜ 时，S△OPQ=8| |=﹣8（ ）=8（﹣1+ 
），
∵0≤k2＜ 时，∴0＜1﹣4k2≤1， ≥2，
∴S△OPQ=8（﹣1+ ）≥8，当且仅当k=0时取等号，
∴当k=0时，S△OPQ的最小值为8，
综上可知当直线l与椭圆C在四个顶点处相切时，三角形OPQ的面积存在最小值为8．
【解析】（1）根据条件求出a，b即可求椭圆C的方程；（2）联立直线方程和椭圆方程，求出原点到直线的距离，结合三角形的面积公式进行求解即可．
【考点精析】认真审题，首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴：
，焦点在y轴：
)．
