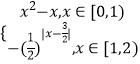题目内容
【题目】下列说法正确的是(只填正确说法序号)
①若集合A={y|y=x﹣1},B={y|y=x2﹣1},则A∩B={(0,﹣1),(1,0)};
② ![]() 是函数解析式;
是函数解析式;
③ ![]() 是非奇非偶函数;
是非奇非偶函数;
④设二次函数f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),则f(x1+x2)=c.
【答案】④
【解析】解:①由集合A={y|y=x﹣1}=R,B={y|y=x2﹣1}=[﹣1,+∞),则A∩B=[﹣1,+∞),因此不正确;
②由 ![]() ,解得x∈,因此
,解得x∈,因此 ![]() 不是函数解析式,不正确;
不是函数解析式,不正确;
③由 ![]() ,解得﹣1≤x≤1,且x≠0,∴函数的定义域为{x|﹣1≤x≤1,且x≠0},关于原点对称.∴
,解得﹣1≤x≤1,且x≠0,∴函数的定义域为{x|﹣1≤x≤1,且x≠0},关于原点对称.∴ ![]() =
= ![]() =f(x),满足f(﹣x)=﹣f(x),因此是奇函数,故不正确;
=f(x),满足f(﹣x)=﹣f(x),因此是奇函数,故不正确;
④设二次函数f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),则x1+x2= ![]() =
= ![]() .∴f(x1+x2)=
.∴f(x1+x2)= ![]() =
= ![]() +b×
+b× ![]() +c=c,因此正确.
+c=c,因此正确.
综上可得:只有④正确.
所以答案是:④.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某学校高一 、高二 、高三三个年级共有 ![]() 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了![]() 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小. (结论不要求证明)
的大小. (结论不要求证明)