题目内容
(本题满分14分)
已知直线
 ,圆
,圆 .
.
(Ⅰ)证明:对任意 ,直线
,直线 与圆
与圆 恒有两个公共点.
恒有两个公共点.
(Ⅱ)过圆心 作
作 于点
于点 ,当
,当 变化时,求点
变化时,求点 的轨迹
的轨迹 的方程.
的方程.
(Ⅲ)直线 与点
与点 的轨迹
的轨迹 交于点
交于点 ,与圆
,与圆 交于点
交于点 ,是否存在
,是否存在 的值,使得
的值,使得 ?若存在,试求出
?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(Ⅰ)见解析;(Ⅱ)轨迹 的方程为
的方程为 .
.
(Ⅲ)存在 ,使得
,使得 且
且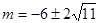 .
.
【解析】本试题主要是考查了直线与圆的位置关系的综合运用。
解:(Ⅰ)方法1:圆心 的坐标为
的坐标为 ,半径为3…………………1分
,半径为3…………………1分
圆心 到直线
到直线 距离
距离 ………………2分
………………2分
∴
∴ 即
即
∴直线 与圆
与圆 恒有两个公共点……………………4分
恒有两个公共点……………………4分
方法2:联立方程组 …………………………1分
…………………………1分
消去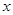 ,得
,得 ………………2分
………………2分

∴直线 与圆
与圆 恒有两个公共点………………………4分
恒有两个公共点………………………4分
方法3:将圆 化成标准方程为
化成标准方程为 .…1分
.…1分
由 可得:
可得: .
.
解 得
得 ,所以直线
,所以直线 过定点
过定点 .……………3分
.……………3分
因为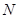 在圆C内,所以直线
在圆C内,所以直线 与圆
与圆 恒有两个公共点.………………4分
恒有两个公共点.………………4分
(Ⅱ)设 的中点为
的中点为 ,由于
,由于 °,
°,
∴
∴ 点的轨迹
点的轨迹 为以
为以 为直径的圆.………………7分
为直径的圆.………………7分
 中点
中点 的坐标为
的坐标为 ,
, .
.
∴所以轨迹 的方程为
的方程为 .………………9分
.………………9分
(Ⅲ)假设存在 的值,使得
的值,使得 .
.
如图所示,
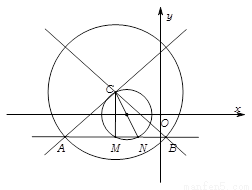
有



 ,……10分
,……10分
又 ,
, ,
,
其中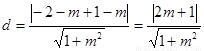 为C到直线
为C到直线 的距离.……………12分
的距离.……………12分
所以 ,化简得
,化简得 .解得
.解得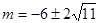 .
.
所以存在 ,使得
,使得 且
且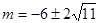 .……………………14分
.……………………14分

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).