题目内容
已知定义在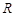 上的函数
上的函数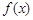 满足
满足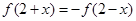 ,当
,当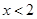 时,
时,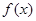 单调递增,若
单调递增,若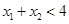 且
且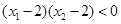 ,则
,则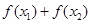 的值( )
的值( )
A.可能为0 B.恒大于0 C.恒小于0 D.可正可负
【答案】
C
【解析】
试题分析:根据题意,由于定义在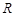 上的函数
上的函数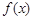 满足
满足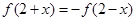 ,则说明函数关于(2,0)呈对称中心图象,那么当
,则说明函数关于(2,0)呈对称中心图象,那么当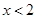 时,
时,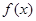 单调递增,x>2,函数递减,那么
单调递增,x>2,函数递减,那么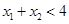 且
且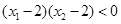 ,则可知
,则可知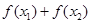 恒小于0,故可知选C.
恒小于0,故可知选C.
考点:函数的单调性
点评:主要是考查了函数的单调性的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






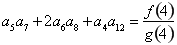

 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则 的取值范围是
( )
的取值范围是
( ) B.
B.
 D.
D.
 上的函数
上的函数 满足
满足 ,且
,且 ,
,
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于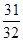 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
(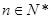 )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于