题目内容
已知定义在 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于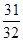 ,则
,则 等于( )
等于( )
A.4 B.6 C.5 D.7
【答案】
C
【解析】
试题分析:令
 ,因为
,因为 ,则
,则
 ,所以
,所以 在R上是单调递减的,所以0<a<1,因为
在R上是单调递减的,所以0<a<1,因为 ,所以
,所以 或 a=2(舍去)。
或 a=2(舍去)。
所以有穷数列 (
( )是以
)是以 为首项,
为首项, 为公比的等比数列,因为有穷数列
为公比的等比数列,因为有穷数列 (
( )的前
)的前 项和等于
项和等于 ,所以
,所以 ,解
,解 。
。
考点:指数函数的性质;导数的运算公式及运算法则;利用导数研究函数的单调性;数列的前n项和;无穷数列的前n项和公式。
点评:本题考查数列与函数的综合,考查导数知识的运用。其难点为构造函数 =
=  ,且判断出
,且判断出 在R上是单调递减的。确定有穷数列
在R上是单调递减的。确定有穷数列 (
( )是以
)是以 为首项,
为首项, 为公比的等比数列是关键.此题属于较难题目。
为公比的等比数列是关键.此题属于较难题目。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






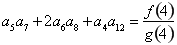

 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则 的取值范围是
( )
的取值范围是
( ) B.
B.
 D.
D.
 上的函数
上的函数 满足
满足 ,且
,且 ,
,
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
(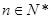 )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于