题目内容
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若
,若 是正项等比数列,且
是正项等比数列,且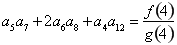 ,则
,则 等于 .
等于 .
【答案】

【解析】
试题分析:∵ ,因为
,因为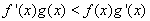 ,∴
,∴ ,即函数
,即函数 单调递减,∴
单调递减,∴ ,又
,又 ,即
,即 ,即,解得
,即,解得 (舍去)或
(舍去)或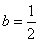 ,∴
,∴ ,即
,即 ,因为
,因为 是正项等比数列,且
是正项等比数列,且 ,故
,故 ,所以
,所以 .
.
考点:导数的运算;等比数列的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则 的取值范围是
( )
的取值范围是
( ) B.
B.
 D.
D.
 上的函数
上的函数 满足
满足 ,且
,且 ,
,
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于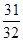 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
(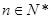 )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于