设函数f(x)＝x2+mx.则下列命题中的真命题是 A．任意m∈R.使y＝f(x)都是奇函数 B．存在m∈R.使y＝f(x)是奇函数 C．任意m∈R.使y＝f(x)都是偶函数 D．存在m∈R.使y＝f(x)是偶函数题目和参考答案——青夏教育精英家教网——

题目内容

设函数f(x)＝x²＋mx(m∈R)，则下列命题中的真命题是（）

A．任意m∈R，使y＝f(x)都是奇函数 B．存在m∈R，使y＝f(x)是奇函数

C．任意m∈R，使y＝f(x)都是偶函数 D．存在m∈R，使y＝f(x)是偶函数

【答案】

D

【解析】

试题分析：函数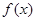首先是二次函数，不可能是奇函数，当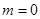时，它是偶函数，当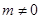时，它也不是偶函数.故选D.

考点：函数的奇偶性.

练习册系列答案

名师点睛教材详解系列答案

课堂精练解读与指导系列答案

初中语文阅读专题训练系列答案

本土好学生小升初系统总复习系列答案

周自主读本系列答案

初中学业考试总复习系列答案

综合素质测评卷系列答案

新课标中学区域地理系列答案

四清导航早读手册系列答案

一本好题口算题卡系列答案

相关题目

设函数f(x)＝x²＋mx(m∈R)，则下列命题中的真命题是 (　　)．

A．任意m∈R，使y＝f(x)都是奇函数

B．存在m∈R，使y＝f(x)是奇函数

C．任意m∈R，使y＝f(x)都是偶函数

D．存在m∈R，使y＝f(x)是偶函数

设函数f(x)＝x²－1＋cosx(a>0)．

(1)当a＝1时，证明：函数y＝f(x)在(0，＋∞)上是增函数；

(2)若y＝f(x)在(0，＋∞)上是单调增函数，求正数a的范围．

对实数a和b，定义运算“⊕”：a⊕b＝设函数f(x)＝(x²－2)⊕(x－x²)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是

A．(－∞，－2]∪ B．(－∞，－2]∪

C. ∪ D. ∪

、（12分）设函数f(x) ＝ x2＋bln(x＋1),

（1）若对定义域的任意x，都有f(x)≥f(1)成立，求实数b的值；

（2）若函数f(x)在定义域上是单调函数，求实数b的取值范围；

（3）若b＝－1，证明对任意的正整数n，不等式成立；

设函数f(x)＝x²＋3，对任意x∈[1，＋∞)，f()＋m²f(x)≥f(x－1)＋3f(m)恒成立，则实数m的取值范围是　　　　　　　　　　　　　.