题目内容
14.设z是复数,则下列命题中的真命题是( )| A. | 若z2<0,则|z|=-z+i | B. | 若z2<0,则$\frac{z}{1+i}$的共轭虚数$\frac{z}{i-1}$ | ||
| C. | 若z是虚数,则z2≥0 | D. | 若z2≥0,则$\frac{z}{1+i}$的共轭虚数$\frac{z}{i-1}$ |
分析 设出z=a+bi,通过复数的运算性质以及共轭复数的定义进行判断即可.
解答 解:设z=a+bi,z2=a2-b2+2abi,
若z2<0,则a=0,
∴z=bi,∴|z|=b,而-z+i是虚数,
故A错误;
$\frac{z}{1+i}$=$\frac{bi}{1+i}$=$\frac{b}{2}$+$\frac{b}{2}$i,而$\frac{z}{i-1}$=$\frac{bi}{i-1}$=$\frac{b}{2}$-$\frac{b}{2}$i,是共轭复数,
故B正确;
若z是虚数,则z2>0,故C错误;
若z2≥0,则b=0,z=a,是实数,故D错误;
故选:B.
点评 本题考查了复数的运算性质,考查共轭复数的定义,是一道基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
5.已知$a={0.5^{\frac{1}{3}}},b={0.3^{\frac{1}{3}}},c={log_{0.3}}0.2$,则a、b、c的大小关系是( )
| A. | c<b<a | B. | a<b<c | C. | b<a<c | D. | a<c<b |
3.下列命题中,真命题是( )
| A. | ?x0∈[0,$\frac{π}{2}$],sin x0+cos x0≥2 | B. | ?x∈(3,+∞),x2>2x+1 | ||
| C. | ?x0∈R,x02+x0=-1 | D. | ?x∈($\frac{π}{2}$,π),tan x>sin x |
 如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.
如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.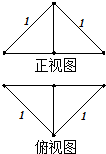 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.