题目内容
如图,在四棱锥 中,
中, ,
, ,且DB平分
,且DB平分 ,
,
E为PC的中点, ,
,
(Ⅰ)证明
(Ⅱ)证明
(Ⅲ)求直线BC与平面PBD所成的角的正切值
 中,
中, ,
, ,且DB平分
,且DB平分 ,
,E为PC的中点,
 ,
,
(Ⅰ)证明

(Ⅱ)证明

(Ⅲ)求直线BC与平面PBD所成的角的正切值

证明见解析 (3)正切值为 。
。
 。
。 (Ⅰ)要证明 只需证明
只需证明 E为PC的中点,在找一中点,构成中位线,得出平行;
E为PC的中点,在找一中点,构成中位线,得出平行;
(Ⅱ)证明 ,因为
,因为 所以
所以 ,
,
再找
BC在平面PBD内的射影,做垂线BH,也可证明,BH为BC在平面PBD内的射影,所以 为直线与平面PBD所成的角。
为直线与平面PBD所成的角。
证明:设 ,连结EH,在
,连结EH,在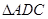 中,因为AD=CD,且DB平分
中,因为AD=CD,且DB平分 ,所以H为AC的中点,又有题设,E为PC的中点,故
,所以H为AC的中点,又有题设,E为PC的中点,故 ,又
,又
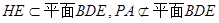 ,所以
,所以
(2)证明:因为 ,
, ,所以
,所以
由(1)知,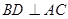 ,
, 故
故
(3)解:由 可知,BH为BC在平面PBD内的射影,所以
可知,BH为BC在平面PBD内的射影,所以 为直线与平面PBD所成的角。
为直线与平面PBD所成的角。
由 ,
,
在 中,
中, ,所以直线BC与平面PBD所成的角的正切值为
,所以直线BC与平面PBD所成的角的正切值为 。
。
 只需证明
只需证明 E为PC的中点,在找一中点,构成中位线,得出平行;
E为PC的中点,在找一中点,构成中位线,得出平行;(Ⅱ)证明
 ,因为
,因为 所以
所以 ,
,再找

BC在平面PBD内的射影,做垂线BH,也可证明,BH为BC在平面PBD内的射影,所以
 为直线与平面PBD所成的角。
为直线与平面PBD所成的角。证明:设
 ,连结EH,在
,连结EH,在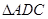 中,因为AD=CD,且DB平分
中,因为AD=CD,且DB平分 ,所以H为AC的中点,又有题设,E为PC的中点,故
,所以H为AC的中点,又有题设,E为PC的中点,故 ,又
,又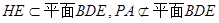 ,所以
,所以
(2)证明:因为
 ,
, ,所以
,所以
由(1)知,
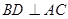 ,
, 故
故
(3)解:由
 可知,BH为BC在平面PBD内的射影,所以
可知,BH为BC在平面PBD内的射影,所以 为直线与平面PBD所成的角。
为直线与平面PBD所成的角。由
 ,
,
在
 中,
中, ,所以直线BC与平面PBD所成的角的正切值为
,所以直线BC与平面PBD所成的角的正切值为 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目













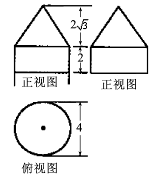


 (
( )角,且该平面与圆柱的侧面相交,则它们的交线是一个椭圆. 当
)角,且该平面与圆柱的侧面相交,则它们的交线是一个椭圆. 当
 时,椭圆的离心率是
时,椭圆的离心率是