Question

（2013•浦东新区二模）已知以4为周期的函数f(x)=

m(1-|x|)，x∈(-1，1] -cos πx 2 ， x∈(1，3]

其中m＞0，若方程f(x)=

x

3

恰有5个实数解，则m的取值范围为（　　）

• A．(

  4

  3

  ，+∞)
• B．[

  4

  3

  ，+∞)
• C．(

  4

  3

  ，

  8

  3

  )
• D．[

  4

  3

  ，

  8

  3

  ]

Answer 1

分析：根据对函数的解析式画出函数的图象，结合方程f(x)=

x

3

恰有5个实数解，即函数y=f（x）与y=

x

3

的图象有且只有五个交点，在同一坐标系中画出两个函数的图象，数形结合，可分析出m的取值范围．

解答：解：∵若方程f(x)=

x

3

恰有5个实数解，
则函数f(x)=

m(1-|x|)，x∈(-1，1] -cos πx 2 ， x∈(1，3]

的图象与y=

x

3

的图象有且只有五个交点，
在同一坐标系中画出函数y=f（x）与y=

x

3

的图象如下图所示：

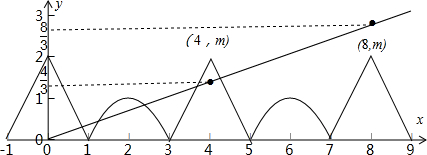
由图可得：m∈(

4

3

，

8

3

)
故选C

点评：本题主要考查了函数的周期性．采用了数形结合的方法，很直观．