题目内容
设x，y∈R，且x2+y2=4，则
的最大值是（ ）A．
B．
C．2
D．4
【答案】分析：根据题意，x2+y2=4，则可设x=2sinα，y=2cosα，将其代入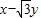
可得t=
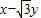=2sinα-2
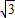cosα，由正弦的差角公式将t变形为4sin（α-
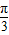），由三角函数的性质易得答案．
解答：解：根据题意，x2+y2=4，则可设x=2sinα，y=2cosα，t=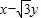
；
则t=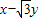
=2sinα-2
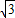cosα=4（
sinα-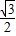
cosα）=4sin（α-
），
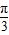易得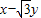
的最大值是4，
故选D．
点评：本题考查函数的最值，用换元法结合三角函数的恒等变形解题，转化为三角函数的最值，可以简化运算．
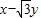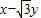可得t==2sinα-2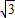cosα，由正弦的差角公式将t变形为4sin（α-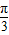），由三角函数的性质易得答案．解答：解：根据题意，x2+y2=4，则可设x=2sinα，y=2cosα，t=
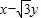；则t=
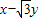=2sinα-2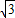cosα=4（sinα-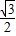cosα）=4sin（α-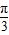），易得
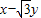的最大值是4，故选D．
点评：本题考查函数的最值，用换元法结合三角函数的恒等变形解题，转化为三角函数的最值，可以简化运算．
练习册系列答案
相关题目