题目内容
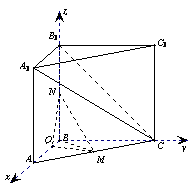
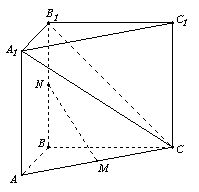 如图,在直三棱柱
如图,在直三棱柱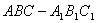 中,
中,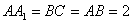 ,
,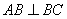 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。
(1)求二面角 的大小。
的大小。
(2)证明:在AB上存在一个点Q,使得平面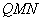 ⊥平面
⊥平面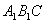 ,并求出
,并求出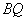 的长度。
的长度。
【答案】
解:方法一(向量法)
如图建立空间直角坐标系……………………1分
(1)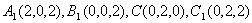
∴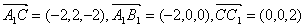
设平面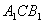 的法向量为
的法向量为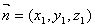 ,平面
,平面 的法向量为
的法向量为
则有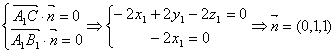 …………3分
…………3分
 …………5分
…………5分
 设二面角
设二面角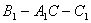 为θ,则
为θ,则

∴二面角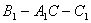 的大小为60°。…………7分
的大小为60°。…………7分
(2)设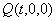 ………………9分
………………9分
∵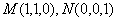
∴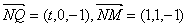 ,设平面
,设平面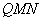 的法向量为
的法向量为
则有: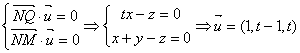 …………11分
…………11分
由(1)可知平面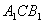 的法向量为
的法向量为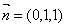
∵平面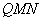 ⊥平面
⊥平面
∴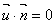 即
即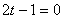 ,
,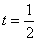
此时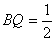 。………………14分
。………………14分
方法二:(1)取 中点
中点 ,连接
,连接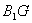
 ∵
∵ ∴
∴
又∵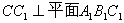 ∴
∴
∴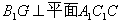 ∴
∴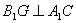
过 做
做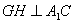 于H,连接
于H,连接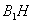
∴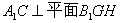 ∴
∴
∴ 为二面角
为二面角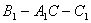 的平面角………………4分
的平面角………………4分
有: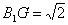
∵ ∽
∽ ,
, ,
,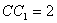 ,
,
∴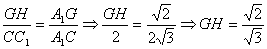
∴
∴ …………………………7分
…………………………7分
(2)同方法一

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
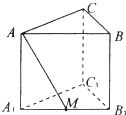 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1= 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
 中,
中, ,
, 分别为
分别为 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形. 平面
平面 ;
; 平面
平面 的余弦值.
的余弦值.
 中,
中, ,
, ,
, 是
是 的中点.
的中点. ∥平面
∥平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定
 中,
中, ,点
,点 是
是 的中点.
的中点. ;(2)
;(2) 平面
平面 .
.