题目内容
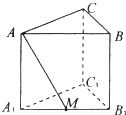 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=| 2 |
分析:以C1点坐标原点,C1A1,C1B1,C1C分别为X,Y,Z轴正方向建立空间坐标系,分另求出直线AM的方向向量与平面AA1C1C的法向量,代入向量夹角公式,即可求出AM与平面AA1C1C所成角的正切值.
解答:解:以C1点坐标原点,C1A1,C1B1,C1C分别为X,Y,Z轴正方向建立空间坐标系,
则∵AC=BC=1,侧棱AA1=
,M为A1B1的中点,
∴
=(-
,
,-
),
=(0,-1,0)为平面AA1C1C的一个法向量
设AM与平面AA1C1C所成角为θ,
则sinθ=|
|=
则tanθ=
故答案为:
则∵AC=BC=1,侧棱AA1=
| 2 |
∴
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| BC |
设AM与平面AA1C1C所成角为θ,
则sinθ=|
| ||||
|
|
| ||
| 10 |
则tanθ=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查的知识点是直线与平面所成的角,其中建立坐标系,求出直线的方向向量和平面的法向量,将线面夹角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
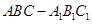 中, AB=1,
中, AB=1,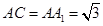 ,
,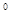 .
.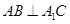 ;
;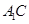 —B的正切值。
—B的正切值。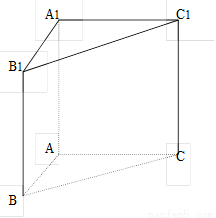
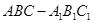 中,
中,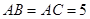 ,
,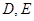 分别为
分别为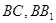 的中点,四边形
的中点,四边形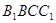 是边长为
是边长为 的正方形.
的正方形.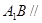 平面
平面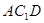 ;
;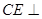 平面
平面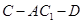 的余弦值.
的余弦值.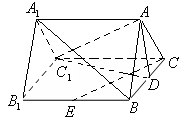
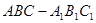 中,
中,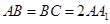 ,
,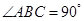 ,
,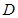 是
是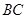 的中点.
的中点.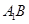 ∥平面
∥平面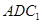 ;
;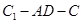 的余弦值;
的余弦值;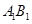 上是否存在点
上是否存在点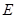 ,使
,使 与
与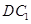 成
成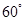 角?若存在,确定
角?若存在,确定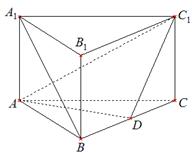
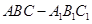 中,
中,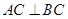 ,点
,点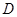 是
是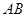 的中点.
的中点.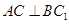 ;(2)
;(2)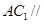 平面
平面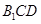 .
.