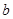题目内容
(本小题满分12分)某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(Ⅰ)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(Ⅱ)设甲篮球运动员10场比赛得分平均值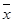 ,将10场比赛得分
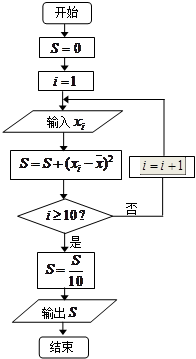
,将10场比赛得分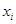 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的 大小为多少?并说明
大小为多少?并说明 的统计学意义;
的统计学意义;
(Ⅲ)如果从甲、乙两位运动员的10场得分中,各随机抽取一场不小于30分的得分,求甲的得分大于乙的得分的概率.
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(Ⅰ)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(Ⅱ)设甲篮球运动员10场比赛得分平均值
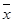 ,将10场比赛得分
,将10场比赛得分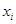 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的 大小为多少?并说明
大小为多少?并说明 的统计学意义;
的统计学意义;
(Ⅲ)如果从甲、乙两位运动员的10场得分中,各随机抽取一场不小于30分的得分,求甲的得分大于乙的得分的概率.
(Ⅰ)见解析(Ⅱ)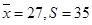 ,意义见解析。(Ⅲ)
,意义见解析。(Ⅲ)
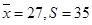 ,意义见解析。(Ⅲ)
,意义见解析。(Ⅲ)
本试题主要是考查了茎叶图和框图的知识的综合运用,以及古典概型的试验空间的问题。
(1)统计结论:
①甲运动员得分的平均值小于乙运动员得分的平均值;
②甲运动员得分比乙运动员得分比较集中;
③甲运动员得分的中位数为27,乙运动员得分的中位数为28.5;
④甲运动员得分基本上是对称的,而且大多数集中在均值附近.乙运动员得分分布较为分散
(2)根据均值公式和方差公式求解得到,并说明。
(3)记甲、乙两位运动员的得分为 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。
解:(Ⅰ)统计结论:①甲运动员得分的平均值小于乙运动员得分的平均值;
②甲运动员得分比乙运动员得分比较集中;
③甲运动员得分的中位数为27,乙运动员得分的中位数为28.5;
④甲运动员得分基本上是对称的,而且大多数集中在均值附近.乙运动员得分分布较为分散.(给分说明:写出的结论中,1个正确得2分)………………5分
(Ⅱ)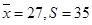 .………………………………………………6分
.………………………………………………6分
 表示10场比赛得分的方差,是描述比赛得分离散程度的量,
表示10场比赛得分的方差,是描述比赛得分离散程度的量, 值越小,表示比赛得分比较集中,
值越小,表示比赛得分比较集中, 值
值
越大,表示比赛得分越参差不齐.…………………………………8分
(Ⅲ)记甲、乙两位运动员的得分为 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为:
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为: ,
, ,
,
 ,
, ,
, ;
;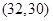 ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ;
;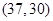 ,
, ,
, ,
, ,
, ;共有20种情况,…10分。
;共有20种情况,…10分。
其中甲的得分大于乙的得分有: ,
,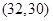 ,
, ,
,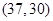 ,共4种情况.………11分
,共4种情况.………11分
从而甲的得分大于乙的得分的概率为 .………………………………12分
.………………………………12分
(1)统计结论:
①甲运动员得分的平均值小于乙运动员得分的平均值;
②甲运动员得分比乙运动员得分比较集中;
③甲运动员得分的中位数为27,乙运动员得分的中位数为28.5;
④甲运动员得分基本上是对称的,而且大多数集中在均值附近.乙运动员得分分布较为分散
(2)根据均值公式和方差公式求解得到,并说明。
(3)记甲、乙两位运动员的得分为
 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。解:(Ⅰ)统计结论:①甲运动员得分的平均值小于乙运动员得分的平均值;
②甲运动员得分比乙运动员得分比较集中;
③甲运动员得分的中位数为27,乙运动员得分的中位数为28.5;
④甲运动员得分基本上是对称的,而且大多数集中在均值附近.乙运动员得分分布较为分散.(给分说明:写出的结论中,1个正确得2分)………………5分
(Ⅱ)
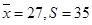 .………………………………………………6分
.………………………………………………6分 表示10场比赛得分的方差,是描述比赛得分离散程度的量,
表示10场比赛得分的方差,是描述比赛得分离散程度的量, 值越小,表示比赛得分比较集中,
值越小,表示比赛得分比较集中, 值
值越大,表示比赛得分越参差不齐.…………………………………8分
(Ⅲ)记甲、乙两位运动员的得分为
 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为:
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为: ,
, ,
, ,
, ,
, ;
;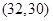 ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ;
;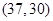 ,
, ,
, ,
, ,
, ;共有20种情况,…10分。
;共有20种情况,…10分。其中甲的得分大于乙的得分有:
 ,
,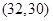 ,
, ,
,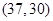 ,共4种情况.………11分
,共4种情况.………11分从而甲的得分大于乙的得分的概率为
 .………………………………12分
.………………………………12分
练习册系列答案
相关题目


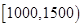 ,
,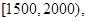
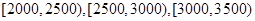 ,
,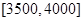 的人数依次为
的人数依次为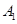 、
、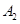 、……、
、……、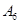 .图乙是统计图甲中月工资收
.图乙是统计图甲中月工资收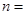 ;图乙
;图乙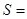 .(用数字作答)
.(用数字作答)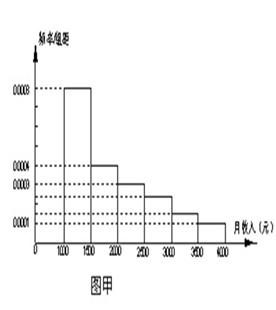

 (含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100
(含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100

 ;
; ;
;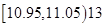 ;
; ;
; ;
; ;
; ;
;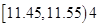 ;
; ;
; 范围内的可能性是百分之几?
范围内的可能性是百分之几? 列联表则表中
列联表则表中 _______,
_______, 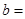 _____________.
_____________.