题目内容
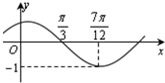已知函数f（x）=Msin（ωx+φ）（其中M＞0，ω＞0，|φ|＜| π |
| 2 |
（1）求函数f（x）的表达式；
（2）设α∈(
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| α |
| 2 |
| 3 |
| 5 |
| β |
| 2 |
| 4 |
| 5 |
分析：（1）根据函数的图象看出振幅和周期，做出ω的值，根据函数过的一个点，把点的坐标代入解析式，根据φ的三角函数值和范围，得到结果．
（2）根据所给的角的范围和角的函数值，求出要用的函数值，这是一个给值求值的过程，最后有角的变换，一个凑角的过程，再根据二倍角公式得到结果．
（2）根据所给的角的范围和角的函数值，求出要用的函数值，这是一个给值求值的过程，最后有角的变换，一个凑角的过程，再根据二倍角公式得到结果．
解答：解：（1）由图知，M=1，∵周期T=4(
-
)=π，
∴ω=
=2∴f（x）=sin（2x+φ）
又∵f(
)=-1，
∴sin(
+φ)=-1，
∴
+φ=2kπ+
(k∈Z)
∴φ=2kπ+
∵|φ|＜
，∴φ=
∴f(x)=sin(2x+
)．
（2）∵f(
)=
， f(
)=-
，
∴sin(α+
)=
， sin(β+
)=-
．
∵α∈(
，
)， β∈(-
，-
)，
∴α+
∈(
， π)， β+
∈(-
， 0)
于是cos(α+
)=-
， cos(β+
)=
．
∵sin(α-β)=sin[(α+
)-(β+
)]=sin(α+
)cos(β+
)-cos(α+
)sin(β+
)=
•
-(-
)•(-
)=-
，
∴cos2(α-β)=1-2sin2(α-β)=1-2×(-
)2=
．
| 7π |
| 12 |
| π |
| 3 |
∴ω=
| 2π |
| π |
又∵f(
| 7π |
| 12 |
∴sin(
| 7π |
| 6 |
∴
| 7π |
| 6 |
| 3π |
| 2 |
∴φ=2kπ+
| π |
| 3 |
∵|φ|＜
| π |
| 2 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
（2）∵f(
| α |
| 2 |
| 3 |
| 5 |
| β |
| 2 |
| 4 |
| 5 |
∴sin(α+
| π |
| 3 |
| 3 |
| 5 |
| π |
| 3 |
| 4 |
| 5 |
∵α∈(
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
∴α+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
于是cos(α+
| π |
| 3 |
| 4 |
| 5 |
| π |
| 3 |
| 3 |
| 5 |
∵sin(α-β)=sin[(α+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 7 |
| 25 |
∴cos2(α-β)=1-2sin2(α-β)=1-2×(-
| 7 |
| 25 |
| 527 |
| 625 |
点评：本题考查三角函数的解析式的求法和给值求值问题，在解题规程中一定要注意角的变换问题，注意把未知的教转化成已知角来应用和求解．
练习册系列答案
相关题目