题目内容
(本题满分12分)
设函数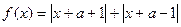 的图象关于y轴对称,函数
的图象关于y轴对称,函数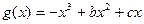 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(1) 求f(x)的表达式;
(2) 试求b的值;
(3) 若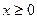 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
设函数
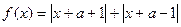 的图象关于y轴对称,函数
的图象关于y轴对称,函数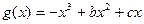 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:(1) 求f(x)的表达式;
(2) 试求b的值;
(3) 若
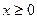 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。解析(1)由函数f(x)的图象关于y轴对称,得f(-1)=f(1),即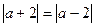 ,解得a=0,所以
,解得a=0,所以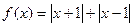
(2)设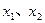 是函数g(x)的两个极值点,则
是函数g(x)的两个极值点,则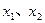 是方程
是方程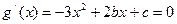 的两个不等实根,则
的两个不等实根,则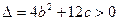 (c为正整数)
(c为正整数) 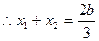
又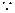 A、O、B三点共线
A、O、B三点共线 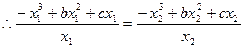
即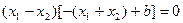 ,又
,又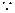
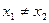 ,
,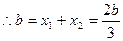 ,
, 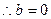
(3)
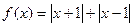
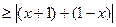 =2
=2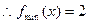
又
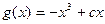 ,令
,令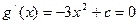 ,
,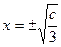
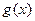 在(
在(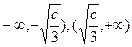 上单
上单 调递减,在
调递减,在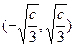 上单调递增
上单调递增
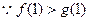
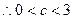
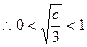 ,满足题意只需
,满足题意只需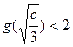
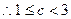 ,即c=1或2
,即c=1或2
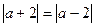 ,解得a=0,所以
,解得a=0,所以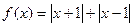
(2)设
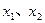 是函数g(x)的两个极值点,则
是函数g(x)的两个极值点,则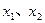 是方程
是方程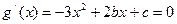 的两个不等实根,则
的两个不等实根,则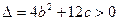 (c为正整数)
(c为正整数) 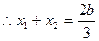
又
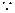 A、O、B三点共线
A、O、B三点共线 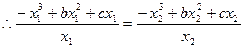
即
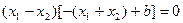 ,又
,又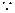
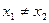 ,
,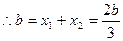 ,
, 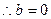
(3)
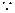
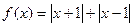
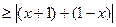 =2
=2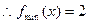
又
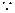
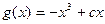 ,令
,令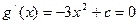 ,
,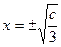
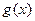 在(
在(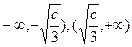 上单
上单 调递减,在
调递减,在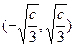 上单调递增
上单调递增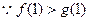
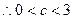
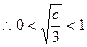 ,满足题意只需
,满足题意只需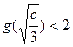
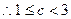 ,即c=1或2
,即c=1或2略

练习册系列答案
相关题目
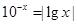 的两根为
的两根为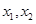 ,则 ( )
,则 ( )



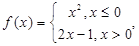 若
若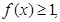 则x的取值范围是
则x的取值范围是



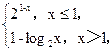 则满足f(x)≤2的x的取值范围是( )
则满足f(x)≤2的x的取值范围是( ) )
)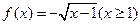 的反函数是 .
的反函数是 .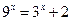 的解为 ▲ .
的解为 ▲ .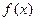 的定义域为
的定义域为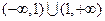 ,且
,且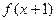 为奇函数,当
为奇函数,当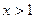 时,
时, 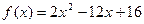 ,则直线
,则直线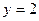 与函数
与函数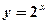 与
与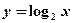 的图像关于直线
的图像关于直线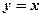 对称;②为了得到函数
对称;②为了得到函数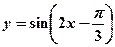 的图象,只需把函数
的图象,只需把函数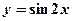 的图象上的所有点向右平移
的图象上的所有点向右平移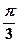 个单位长度; ③当
个单位长度; ③当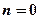 或
或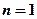 时,
时, 幂函数
幂函数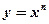 的图象都是一条直线;④已知函数
的图象都是一条直线;④已知函数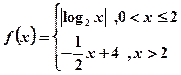 ,
, 若
若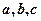 互不相等,且
互不相等,且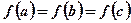 ,则
,则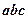 的取值
的取值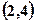 .
. 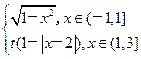 其中t>0.若函数y=
其中t>0.若函数y=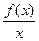 -
-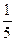 的零点个数是5,则t的取值范
的零点个数是5,则t的取值范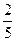 ,1)
,1)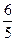 )
)