题目内容
(10分)设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)证明 在区间
在区间 内单调递增;
内单调递增;
(3)若对于区间[3,4]上的每一个 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)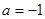 (2)证明见解析(3)
(2)证明见解析(3)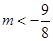
解析试题分析:(1)∵ f(-x)=-f(x),∴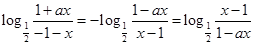 .
.
∴  ,即
,即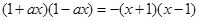 ,∴a=-1. ……3分
,∴a=-1. ……3分
(2)由(1)可知f(x)=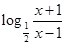
 (x>1) 记u(x)=1+
(x>1) 记u(x)=1+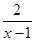 ,
,
由定义可证明u(x)在(1,+∞)上为减函数, ∴ f(x)=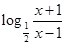 在(1,+∞)上为增函数. ……6分
在(1,+∞)上为增函数. ……6分
(3)设g(x)=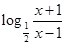 -
-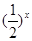 .则g(x)在[3,4]上为增函数. ∴g(x)>m对x∈[3,4]恒成立,∴
.则g(x)在[3,4]上为增函数. ∴g(x)>m对x∈[3,4]恒成立,∴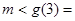 -
-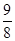 . ……10分
. ……10分
考点:本小题主要考查利用函数的奇偶性求参数值、利用定义证明单调性和不等式恒成立问题求参数的取值范围,
点评:考查函数的性质要先看函数的定义域,证明单调性要用定义,恒成立问题一般转化为最值问题解决.

练习册系列答案
相关题目
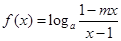
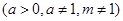 是奇函数.
是奇函数. 的值;
的值;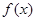 在
在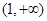 上的单调性,并给出证明;
上的单调性,并给出证明;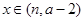 时,函数
时,函数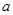 与
与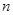 的值。
的值。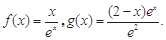
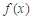 的极值;
的极值;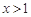 时,
时,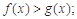
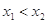 ,且
,且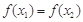 ,求证:
,求证: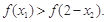
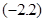 上的奇函数
上的奇函数 ,满足
,满足 ,又当
,又当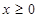 时,
时,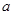 的取值范围。
的取值范围。 的最小值为1,且
的最小值为1,且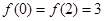 .
.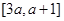 上不单调,求实数
上不单调,求实数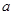 的取值范围;
的取值范围;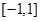 上,
上,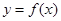 的图象恒在
的图象恒在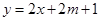 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围.
的取值范围. 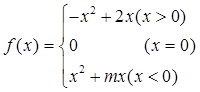
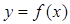 的图象;
的图象; 在区间[-1,
在区间[-1, -2]上单调递增,试确定
-2]上单调递增,试确定
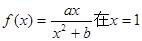 处取得极值2。
处取得极值2。 的解析式;
的解析式;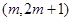 为增函数;
为增函数;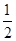 )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),