题目内容
(本小题满分10分)
已知向量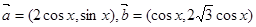 ,函数
,函数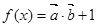 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在 中,
中,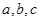 分别是角
分别是角 的对边,
的对边,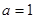 且
且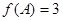 ,求
,求 面积
面积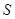 的最大值.
的最大值.
(1) 的单调递增区间为
的单调递增区间为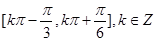
(2)当且仅当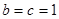 时,
时,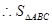 取得最大值
取得最大值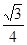 .
.
解析试题分析:(1)
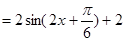 ,
,
由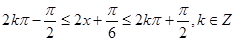
得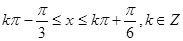 ,
,
所以 的单调递增区间为
的单调递增区间为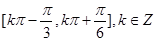
(2)由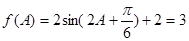 得
得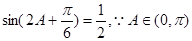 ,
,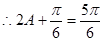 ,即
,即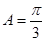 .
.
由余弦定理得 ,
, ,
,
当且仅当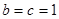 时,
时,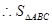 取得最大值
取得最大值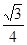 .
.
考点:本题主要考查平面向量的坐标运算,余弦定理的应用,和差倍半的三角函数公式,三角函数图象和性质。
点评:中档题,其中(I)解答思路比较明确,关键是准确进行向量的坐标运算,并运用三角公式化简,进一步研究函数的单调区间。(II)则灵活运用余弦定理并运用正弦函数的有界性,确定得到三角形面积的最大值。

练习册系列答案
相关题目
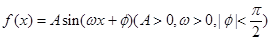 在一个周期内的图像下图所示。
在一个周期内的图像下图所示。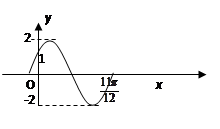
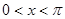 ,且方程
,且方程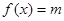 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。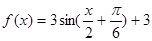 ,
,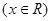
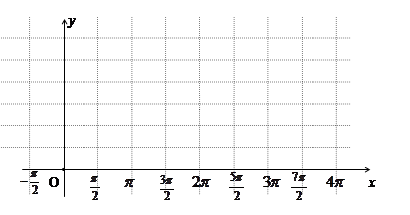
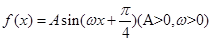 的最大值2,其图象相邻两条对称轴之间的距离为
的最大值2,其图象相邻两条对称轴之间的距离为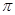 。
。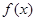 的解析式;
的解析式;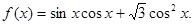
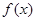 的最小正周期;
的最小正周期;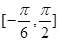 上的最大值和最小值.
上的最大值和最小值. )=
)= 。求cosa
。求cosa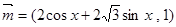 ,
,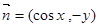 ,满足
,满足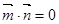 .
. 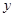 表示为
表示为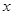 的函数
的函数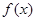 ,并求
,并求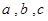 分别为
分别为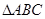 的三个内角
的三个内角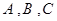 对应的边长,若
对应的边长,若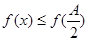 对所有
对所有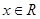 恒成立,且
恒成立,且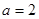 ,求
,求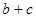 的取值范围.
的取值范围. ,
, . 记
. 记 (其中
(其中 都为常数,且
都为常数,且 ).
).  ,
, ,求
,求 的最大值及此时的
的最大值及此时的 值;
值;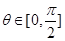 ,①证明:
,①证明: ;②证明:
;②证明: .
. 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为 .
. 的值; (2)求
的值; (2)求 的值.
的值.