题目内容
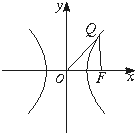 已知△OFQ的面积为2
已知△OFQ的面积为2| 6 |
| OF |
| FQ |
(1)设
| 6 |
| 6 |
| OF |
| FQ |
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),|
| OF |
| ||
| 4 |
| OQ |
分析:(1)利用△OFQ的面积为2
,且
•
=m,可求tanθ的值,根据m的范围,即可求得向量
与
的夹角θ的取值范围;
(2)利用|
|=c,
•
═(
-1)c2,可求|
|,利用基本不等式求最小值,从而可求双曲线的方程.
| 6 |
| OF |
| FQ |
| OF |
| FQ |
(2)利用|
| OF |
| OF |
| FQ |
| ||
| 4 |
| OQ |
解答:解:(1)由已知,△OFQ的面积为2
,且
•
=m,得
(2分)
∴tanθ=
,
∵
<m<4
,∴1<tanθ<4,
∴
<θ<arctan4.(6分)
(2)设所求的双曲线方程为
-
=1,(a>0,b>0),Q(x1,y1),则
=(x1-c,y1)
∵△OFQ的面积
|
||y1|=2
,∴y1=±
,
又由
•
=(c,0)•(x1-c,y1)=(x1-c)c=(
-1)c2,∴x1=
c,(8分)
|
|=
=
≥
,当且仅当c=4时,|
|最小.
此时Q的坐标为(
,
),或(
,-
).
由此可得
,解得
(11分)
故所求方程为
-
=1.(12分)
| 6 |
| OF |
| FQ |
|
∴tanθ=
4
| ||
| m |
∵
| 6 |
| 6 |
∴
| π |
| 4 |
(2)设所求的双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
| FQ |
∵△OFQ的面积
| 1 |
| 2 |
| OF |
| 6 |
4
| ||
| c |
又由
| OF |
| FQ |
| ||
| 4 |
| ||
| 4 |
|
| OQ |
| x12+y12 |
|
| 12 |
| OQ |
此时Q的坐标为(
| 6 |
| 6 |
| 6 |
| 6 |
由此可得
|
|
故所求方程为
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题考查向量知识的运用,考查双曲线标准方程的求解,考查基本不等式的运用,正确运用向量的数量积公式是关键.

练习册系列答案
相关题目
 已知△OFQ的面积为
已知△OFQ的面积为 如图,已知△OFQ的面积为S,且
如图,已知△OFQ的面积为S,且 已知△OFQ的面积为
已知△OFQ的面积为 (2007•天津一模)已知△OFQ的面积为2
(2007•天津一模)已知△OFQ的面积为2