题目内容
20．直线l的方程为（a+1）x+y+2-a=0（a∈R）．（1）若l在两坐标轴上的截距相等，求a的值；
（2）若l不经过第二象限，求实数a的取值范围．
分析 （1）通过讨论2-a是否为0，求出a的值即可；
（2）根据一次函数的性质判断a的范围即可．
解答 解：（1）当直线过原点时，该直线在x轴和y轴上的截距为零，当然相等，
∴a=2，方程即3x+y=0；（2分）
若a≠2，则$\frac{a-2}{a+1}$=a-2，即a+1=1，
∴a=0 即方程为x+y+2=0，
∴a的值为0或2．（6分）
（2）∵过原点时，y=-3x经过第二象限不合题意，
∴直线不过原点（10分）
∴a≤-1．（12分）
点评 本题考查了直线方程问题，考查分类讨论，是一道基础题．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
10．
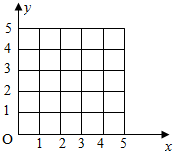某车间为了规定工时定额，需要确定加工某零件所花费的时间，为此作了四次实验，得到的数据如下：
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出y关于x的线性回归方程；
（3）试预测加工10个零件需要多少时间？（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$）
某车间为了规定工时定额，需要确定加工某零件所花费的时间，为此作了四次实验，得到的数据如下：| 零件的个数x（个） | 2 | 3 | 4 | 5 |
| 加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（2）求出y关于x的线性回归方程；
（3）试预测加工10个零件需要多少时间？（注：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$）
11．已知集合M={1，2，3}，N={2，3}，则（ ）
| A． | M=N | B． | M∩N=∅ | C． | M⊆N | D． | N?M |
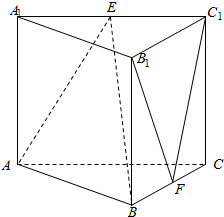在直三棱柱ABC-A1B1C1中，AC=4，CB=2，AA1=2，∠ACB=60°，E、F是A1C1、BC的中点．证明：