题目内容
(2012•开封一模)若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中的真命题是( )
分析:由m、n都平行于平面α,知m,n相交、平行或异面;由m、n为都垂直于平面α,知m、n一定是平行直线;由α、β互相垂直,m、n互相垂直,m⊥α,知n⊥β或n?β;由m、n在平面α内的射影互相垂直,知m、n相交、平行或异面.
解答:解:∵m、n都平行于平面α,
∴m,n相交、平行或异面,
故A不正确;
∵m、n为都垂直于平面α,
∴m、n一定是平行直线,
故B正确;
∵α、β互相垂直,m、n互相垂直,m⊥α,
∴n⊥β或n?β,或C不正确;
∵m、n在平面α内的射影互相垂直,
∴m、n相交、平行或异面,故D不正确.
故选B.
∴m,n相交、平行或异面,
故A不正确;
∵m、n为都垂直于平面α,
∴m、n一定是平行直线,
故B正确;
∵α、β互相垂直,m、n互相垂直,m⊥α,
∴n⊥β或n?β,或C不正确;
∵m、n在平面α内的射影互相垂直,
∴m、n相交、平行或异面,故D不正确.
故选B.
点评:本题考查直线与平面的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
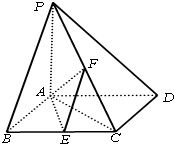 (2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.