题目内容
(2012•开封一模)已知函数h(x)=ln(ax+b)在点M(1,h(1))处的切线方程为x-2y+ln4-1=0.
(Ⅰ)求a,b的值;
(Ⅱ)若f(x)=[h(x)]2-
,求函数f(x)的单调区间.
(Ⅰ)求a,b的值;
(Ⅱ)若f(x)=[h(x)]2-
| x2 | 1+x |
分析:(I)先对函数求导,然后由导数的几何意义可知
=
,h(1)=ln(a+b)=ln2,代入可求a,b
(II)先求函数的定义域为(-1,+∞),f(x)=[h(x)]2-
=ln2(1+x)-
,对函数求导可得f′(x)=
-
=
,构造函数g(x)=2(1+x)ln(1+x)-2x-x2,二次求导,通过导数可得函数g(x)的单调性,进而可得当-1<x<0时,g(x)>g(0)=0,当x>0时,g(x)<g(0)=0,从而可判断函数f(x)的单调区间
| a |
| a+b |
| 1 |
| 2 |
(II)先求函数的定义域为(-1,+∞),f(x)=[h(x)]2-
| x2 |
| 1+x |
| x2 |
| 1+x |
| 2ln(1+x) |
| 1+x |
| x2+2x |
| (1+x)2 |
| 2(1+x)ln(1+x)-x2-2x |
| (1+x)2 |
解答:解(I)∵h(x)=ln(ax+b)
∴h′(x)=
∵在点M(1,h(1))处的切线方程为x-2y+ln4-1=0
∴
=
∵h(1)=ln2即ln(a+b)=ln2
∴a=b=1(4分)
(II)函数的定义域为(-1,+∞),f(x)=[h(x)]2-
=ln2(1+x)-
∴f′(x)=
-
=
设g(x)=2(1+x)ln(1+x)-2x-x2,则g′(x)=2ln(1+x)-2x
令φ(x)=2ln(1+x)-2x,则φ′(x)=
-2=
当-1<x<0时,φ′(x)>0,φ(x)在(-1,0)上单调递增
当x>0时,φ′(x)<0,,φ(x)在(0,+∞)上单调递减
∴,φ(x)在x=0处取得极大值,而,φ(0)=3,
∴g′(x)<0(x≠0)
∴g(x)在(-1,+∞)上单调递减
于是当-1<x<0时,g(x)>g(0)=0,当x>0时,g(x)<g(0)=0
∴当-1<x<0时,f′(x)>0,f(x)在(-1,0)上单调递增
当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减
故函数f(x)的递增区间(-1,0),单调递减区间为(0,+∞)(12分)
∴h′(x)=
| a |
| ax+b |
∵在点M(1,h(1))处的切线方程为x-2y+ln4-1=0
∴
| a |
| a+b |
| 1 |
| 2 |
∵h(1)=ln2即ln(a+b)=ln2
∴a=b=1(4分)
(II)函数的定义域为(-1,+∞),f(x)=[h(x)]2-
| x2 |
| 1+x |
| x2 |
| 1+x |
∴f′(x)=
| 2ln(1+x) |
| 1+x |
| x2+2x |
| (1+x)2 |
| 2(1+x)ln(1+x)-x2-2x |
| (1+x)2 |
设g(x)=2(1+x)ln(1+x)-2x-x2,则g′(x)=2ln(1+x)-2x
令φ(x)=2ln(1+x)-2x,则φ′(x)=
| 2 |
| 1+x |
| -2x |
| 1+x |
当-1<x<0时,φ′(x)>0,φ(x)在(-1,0)上单调递增
当x>0时,φ′(x)<0,,φ(x)在(0,+∞)上单调递减
∴,φ(x)在x=0处取得极大值,而,φ(0)=3,
∴g′(x)<0(x≠0)
∴g(x)在(-1,+∞)上单调递减
于是当-1<x<0时,g(x)>g(0)=0,当x>0时,g(x)<g(0)=0
∴当-1<x<0时,f′(x)>0,f(x)在(-1,0)上单调递增
当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减
故函数f(x)的递增区间(-1,0),单调递减区间为(0,+∞)(12分)
点评:本题主要考察了导数的几何意义的应用,及利用导数求解函数的单调区间,注意本题中利用构造函数二次求导方法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
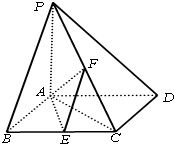 (2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.