题目内容

（2012•开封一模）已知点G是△ABC的重心，若∠A=120°，
AB
•
AC
=-2，则|
AG
|的最小值是
2
3
2
3
．
分析：根据点G是△ABC的重心，故
AG
=
1
3
（
AB
+
AC
），又由∠A=120°，
AB
•
AC
=-2，我们可以求出|
AB
|•|
AC
|=4，进而根据基本不等式，求出|
AB
+
AC
|的取值范围，进而得到|
AG
|的最小值．
解答：解：∵∠A=120°，
AB
•
AC
=-2，
∴|
AB
|•|
AC
|=4，
又∵点G是△ABC的重心，
∴|
AG
|=
1
3
|
AB
+
AC
|=
1
3
(
AB
+
AC
)2
=
1
3
|
AB
|2+|
AC
|2+2
AB
•
AC
≥
1
3
2|
AB
| •|
AC
| +2
AB
•
AC
=
2
3

故答案为：
2
3
点评：本题考查的知识点是向量的模，三角形的重心，基本不等式，其中利用基本不等式求出|
AB
+
AC
|的取值范围是解答本题的关键，另外根据点G是△ABC的重心，得到
AG
=
1
3
（
AB
+
AC
），也是解答本题的关键．
练习册系列答案
相关题目
（2012•开封一模）已知点M（1，0）是圆C：x2+y2-4x-2y=0内一点，则过点M的最长弦所在的直线方程是
x-y-1=0
x-y-1=0
．
（2012•开封一模）已知实数x，y满足条件
x-y+2≥0
0≤x≤3
y≥0
，则目标函数z=2x-y的最大值是
6
6
．
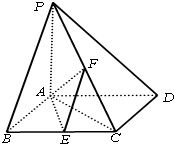（2012•开封一模）已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
（Ⅰ）求证：AE⊥PD；
（Ⅱ）若直线PB与平面PAD所成角的正弦值为
6
4
，求二面角E-AF-C的余弦值．
（2012•开封一模）已知双曲线的渐近线均和圆C：x2+y2-6x+5=0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为
x2
5
-
y2
4
=1
x2
5
-
y2
4
=1
．
（2012•开封一模）已知函数h（x）=ln（ax+b）在点M（1，h（1））处的切线方程为x-2y+ln4-1=0．
（Ⅰ）求a，b的值；
（Ⅱ）若f（x）=[h(x)]2-
x2
1+x
，求函数f（x）的单调区间．
（Ⅲ）求m的取值范围，使不等式(1+
1
n
)n+m≤e对任意的n∈N*都成立（其中e是自然对数的底数）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网