题目内容
已知正方体ABCD-A1B1C1D1中，F是AD的中点，G为AB上一点，若CF⊥FG，则∠C1FG的大小是分析：要证直线与直线垂直可先证直线与平面垂直，根据直线与平面垂直的判定定理可知，FG⊥面FC1C，而FC1?面FC1C，从而得到FG⊥FC1，所求得以解决．
解答：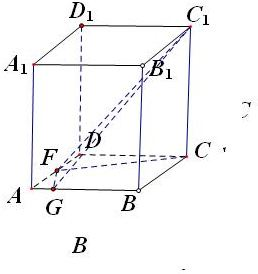
解：如图，∵CF⊥FG，C1C⊥FG，CF∩C1C=C
∴FG⊥面FC1C，而FC1?面FC1C
∴FG⊥FC1，即∠C1FG=
，
故答案为
解：如图，∵CF⊥FG，C1C⊥FG，CF∩C1C=C∴FG⊥面FC1C，而FC1?面FC1C
∴FG⊥FC1，即∠C1FG=
| π |
| 2 |
故答案为
| π |
| 2 |
点评：本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P在平面DD1C1C内，PD1=PC1=
已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．