题目内容
 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.(1)求证:C1O∥面AB1D1;
(2)求异面直线AD1与 C1O所成角的大小.
分析:(1)连接A1C1,设A1C1∩B1D1=O1,连接AO1,利用正方体的性质可证明:AOC1O1是平行四边形.
得到C1O∥AO1,再利用线面平行的判定定理即可得出C1O∥平面AB1D1..
(2)连接BC1,C1D,可得ABC1D1是平行四边形.由于AD1∥BC1,可得∠BC1O为AC1与B1C所成的角.利用正方体的性质可得BC1=C1D=BD.即可得出.
得到C1O∥AO1,再利用线面平行的判定定理即可得出C1O∥平面AB1D1..
(2)连接BC1,C1D,可得ABC1D1是平行四边形.由于AD1∥BC1,可得∠BC1O为AC1与B1C所成的角.利用正方体的性质可得BC1=C1D=BD.即可得出.
解答:证明:(1)连接A1C1,设A1C1∩B1D1=O1,连接AO1,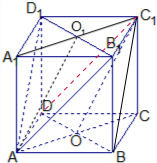
∵ABCD-A1B1C1D1是正方体,
∴A1A
CC1,
∴A1ACC1是平行四边形,
∴A1C1∥AC且 A1C1=AC.
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO,
∴AOC1O1是平行四边形.
∴C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,
∴C1O∥平面AB1D1.
(2)连接BC1,C1D,
∴ABC1D1是平行四边形.
∵AD1∥BC1,
∴∠BC1O为AC1与B1C所成的角.
∵ABCD-A1B1C1D1是正方体,
∴BC1=C1D=BD.
又O是BD的中点,
∴∠BC1O=30°
∴异面直线AD1与 C1O所成角为30°.

∵ABCD-A1B1C1D1是正方体,
∴A1A
| ∥ |
. |
∴A1ACC1是平行四边形,
∴A1C1∥AC且 A1C1=AC.
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO,
∴AOC1O1是平行四边形.
∴C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,
∴C1O∥平面AB1D1.
(2)连接BC1,C1D,
∴ABC1D1是平行四边形.
∵AD1∥BC1,
∴∠BC1O为AC1与B1C所成的角.
∵ABCD-A1B1C1D1是正方体,
∴BC1=C1D=BD.
又O是BD的中点,
∴∠BC1O=30°
∴异面直线AD1与 C1O所成角为30°.
点评:本题考查了正方体的性质、平行四边形的判定定理及其性质定理、等边三角形的性质、线面判定定理、异面直线所成的角等基础知识与基本技能方法,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=