题目内容
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=| 2 |
(1)平面PD1A1⊥平面D1A1BC;
(2)PC1∥平面A1BD.
分析:(1)证明A1D1⊥PD1,PD1⊥D1C,可得PD1⊥平面D1A1BC,利用面面垂直的判定定理,可得结论;
(2)证明PC1∥A1B,利用线面平行的判定定理,可得结论.
(2)证明PC1∥A1B,利用线面平行的判定定理,可得结论.
解答:证明:(1)∵ABCD-A1B1C1D1是正方体,∴A1D1⊥平面DCC1D1,
又点P在平面DD1C1C内,∴A1D1⊥PD1.
∵PD1=PC1=
,且正方体的棱长为2,∴PD1⊥D1C,
又D1C∩A1D1=D1,…(2分)
∴PD1⊥平面D1A1BC,
又PD1?平面PD1A1,
∴平面PD1A1⊥平面D1A1BC. …(4分)
(2)由(1)得,PC1∥D1C,又D1C∥A1B,∴PC1∥A1B. …(6分)
又PC1?平面A1BD,A1B?平面A1BD,∴PC1∥平面A1BD. …(8分)
又点P在平面DD1C1C内,∴A1D1⊥PD1.
∵PD1=PC1=
| 2 |
又D1C∩A1D1=D1,…(2分)
∴PD1⊥平面D1A1BC,
又PD1?平面PD1A1,
∴平面PD1A1⊥平面D1A1BC. …(4分)
(2)由(1)得,PC1∥D1C,又D1C∥A1B,∴PC1∥A1B. …(6分)
又PC1?平面A1BD,A1B?平面A1BD,∴PC1∥平面A1BD. …(8分)
点评:本题考查面面垂直、线面平行的判定定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )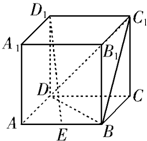 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.