题目内容
17. 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.(Ⅰ)求椭圆的离心率;
(Ⅱ)若△A1MN的外接圆在M处的切线与椭圆相交所得弦长为$\frac{5}{7}$,求椭圆方程.
分析 (Ⅰ)首先,得到点M的坐标,然后,代入,得到$\frac{{\frac{b^2}{a}}}{a+c}=\frac{1}{2}$,从而确定其斜率关系;
(Ⅱ)首先,得到A1(-2c,0)$M(c,\frac{3c}{2})$,然后,可以设外接圆圆心设为P(x0,0),结合圆的性质建立等式,然后,利用弦长公式求解即可.
解答 解:(Ⅰ)由题意$M(c,\frac{b^2}{a})$-------------(1分)
因为A1(-a,0),所以$\frac{{\frac{b^2}{a}}}{a+c}=\frac{1}{2}$-------------(2分)
将b2=a2-c2代入上式并整理得$\frac{a-c}{a}=1-e=\frac{1}{2}$(或a=2c)----------(3分)
所以$e=\frac{1}{2}$------------(4分)
(Ⅱ)由(Ⅰ)得a=2c,$b=\sqrt{3}c$(或$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$)------------(5分)
所以A1(-2c,0)$M(c,\frac{3c}{2})$,外接圆圆心设为P(x0,0)
由|PA1|=|PM|,得$\sqrt{{{({x_0}+2c)}^2}}=\sqrt{{{({x_0}-c)}^2}+{{(\frac{3c}{2})}^2}}$------------(6分)
解得:${x_0}=-\frac{c}{8}$------------(7分)
所以${k_{PM}}=\frac{{\frac{3c}{2}}}{{c+\frac{c}{8}}}=\frac{4}{3}$------------(8分)
所以△A1MN外接圆在M处切线斜率为$-\frac{3}{4}$,设该切线与椭圆另一交点为C
则切线MC方程为$y-\frac{3c}{2}=-\frac{3}{4}(x-c)$,即$y=-\frac{3}{4}x+\frac{9c}{4}$------------(9分)
与椭圆方程3x2+4y2=12c2联立得7x2-18cx+11c2=0------------(10分)
解得${x_1}=c,{x_2}=\frac{11c}{7}$------------(11分)
由弦长公式$|{MC}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$得$\sqrt{1+{{({-\frac{3}{4}})}^2}}|c-\frac{11c}{7}|=\frac{5}{7}$------------(12分)
解得c=1------------(13分)
所以椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$------------(14分)
点评 本题重点考查了椭圆的标准方程、简单几何性质、直线与椭圆的位置关系、弦长公式等知识,属于中档题.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | -1 | B. | 0 | C. | 1 | D. | i |
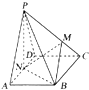 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
 如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.