题目内容
9. 如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
分析 先从图中求出切点,再求出直线l的方程,利用导数在切点处的导数值为切线的斜率,最后结合导数的运算法则,求出g′(3)的值.
解答 解:∵直线l:y=kx+2是曲线y=f(x)在x=3处的切线,
∴f(3)=1,
又点(3,1)在直线l上,
∴3k+2=1,从而k=-$\frac{1}{3}$,
∴f′(3)=k=-$\frac{1}{3}$,
∵g(x)=xf(x),
∴g′(x)=f(x)+xf′(x)
则g′(3)=f(3)+3f′(3)=1+3×(-$\frac{1}{3}$)=0
故答案为:0.
点评 本题考查导数的几何意义:函数在切点处的导数值为曲线的切线的斜率,正确求导是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.某书店订购一本新版图书,根据以往经验预测,这本新书的预售量为40,100,120(本)的概率分别为0.2,0.7,0.1,这本书的订购价为6元,销售价为8元,如果售不出去,以每本为5元的价格处理书,试用盈利决定书店应订购多少本新书?
| 自然状况 | 概率\盈利(元)\方案 | 订购40本 | 订购100本 | 订购120本 |
| 销售40本 | 0.2 | |||
| 销售100本 | 0.7 | |||
| 销售120本 | 0.1 |
4.“a=1“是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
14. 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{3}$ |
1.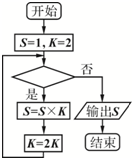 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
 如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )
如图所示的程序框图表示求算式“2×4×8×16×32×64”的值,则判断框内可以填入( )| A. | k<132? | B. | k<70? | C. | k<64? | D. | k<63? |
18.已知F为抛物线C:y2=4x的焦点,点E在C的准线上,且在x轴上方,线段EF的垂直平分线与C的准线交于点Q(-1,$\frac{3}{2}$),与C交于点P,则点P的坐标为( )
| A. | (1,2) | B. | (2,2$\sqrt{2}$) | C. | (3,2$\sqrt{3}$) | D. | (4,4) |
19.已知a=$\int_0^{\frac{π}{2}}{(-cosx)dx}$,则${({ax+\frac{1}{2ax}})^9}$展开式中,x3项的系数为( )
| A. | $\frac{63}{8}$ | B. | $\frac{63}{16}$ | C. | $-\frac{21}{2}$ | D. | $-\frac{63}{8}$ |
 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.