题目内容
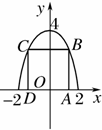
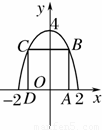
已知矩形的两个顶点位于x轴上，另两个顶点位于抛物线y=4-x2在x轴上方的曲线上，求这个矩形面积最大时的边长。
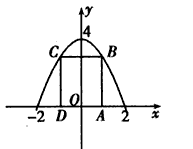
解：设矩形边长AD=2x，则|AB|=y=4-x2，
则矩形面积为S=2x（4-x2）（0＜x＜2），
即S=8x-2x3， S′=8-6x2，
令S′=0，解得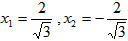
（舍去），
当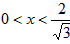
时，S′＞0；
当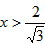
时，S′＜0，
所以当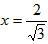
时，S取得最大值，
此时，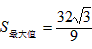
，
即矩形的边长分别为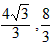
时，矩形的面积最大。
则矩形面积为S=2x（4-x2）（0＜x＜2），
即S=8x-2x3， S′=8-6x2，
令S′=0，解得
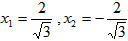（舍去），当
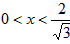时，S′＞0；当
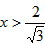时，S′＜0，所以当
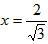时，S取得最大值，此时，
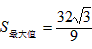，即矩形的边长分别为
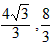时，矩形的面积最大。 
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
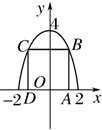已知矩形的两个顶点位于x轴上，另两个顶点位于抛物线y=4-x2在x轴上方的曲线上，则矩形的面积最大为
