题目内容
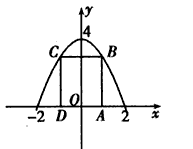
已知矩形的两个顶点位于x轴上，另两个顶点位于抛物线y=4-x2在x轴上方的曲线上，则矩形的面积最大为 ．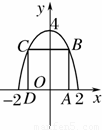
【答案】分析：先设点B的坐标，将面积S表达为变量的函数，再利用导数法求出函数的最大值．
解答：解：设点B（x，4-x2） （O＜x≤2），则S=2x（4-x2）=2x3+8x
∴S′=-6x2+8，令S′=-6x2+8=0，可得x=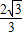
∵O＜x≤2，∴由S′＞0，可得0＜x＜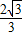
；由S′＜0，可得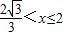
∴x=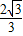
时，S=2x3+8x取得最大值为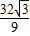
故答案为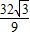
点评：本题解题的关键是利用点在抛物线上设点，从而构建函数，由于函数是单峰函数，所以在导数为0处一定取最值．
解答：解：设点B（x，4-x2） （O＜x≤2），则S=2x（4-x2）=2x3+8x
∴S′=-6x2+8，令S′=-6x2+8=0，可得x=
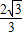
∵O＜x≤2，∴由S′＞0，可得0＜x＜
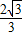；由S′＜0，可得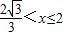∴x=
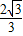时，S=2x3+8x取得最大值为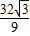故答案为
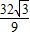
点评：本题解题的关键是利用点在抛物线上设点，从而构建函数，由于函数是单峰函数，所以在导数为0处一定取最值．
练习册系列答案
智慧小复习系列答案
相关题目
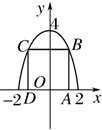已知矩形的两个顶点位于x轴上，另两个顶点位于抛物线y=4-x2在x轴上方的曲线上，则矩形的面积最大为