题目内容
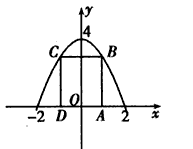
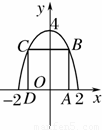
已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y =4-x2在x轴上方的曲线上,则这种矩形中面积最大者的边长为 .
【答案】
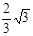 和
和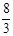 .
.
【解析】
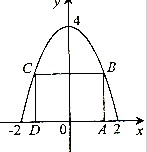
试题分析:设点B(x,4-x2) (O<x≤2)…(1分)
则S=2x(4-x2)=2x3+8x…(3分)
∴S′=-6x2+8,∴S′=-6x2+8=0即x=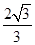 ,另一边长为
,另一边长为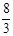 时,S=2x3+8x取得最大值。
时,S=2x3+8x取得最大值。
考点:本题主要考查函数模型、导数的应用。
点评:解题的关键是利用点在抛物线上设点,从而构建函数,由于函数是单峰函数,所以在导数为0处一定取最值。

练习册系列答案
相关题目
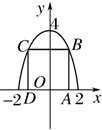 已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y=4-x2在x轴上方的曲线上,则矩形的面积最大为
已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y=4-x2在x轴上方的曲线上,则矩形的面积最大为