题目内容
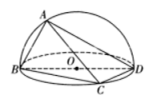
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 都是边长为2的正方形,点
都是边长为2的正方形,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,二面角
的中点,二面角![]() 的大小为60°.
的大小为60°.
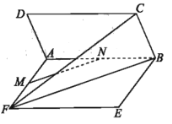
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据三角形的中位线,有![]() ,再利用线面平行的判定定理证明.
,再利用线面平行的判定定理证明.
(2)根据点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,二面角
的中点,二面角![]() 的大小为60°,证明
的大小为60°,证明![]() 平面
平面![]() ,然后以点
,然后以点![]() 为原点,
为原点,![]() ,
,![]() (
(![]() 是
是![]() 中点),
中点),![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图空间直角坐标系,再求得平面
轴建立如图空间直角坐标系,再求得平面![]() 的一个法向量,利用线面角的向量求法求解.
的一个法向量,利用线面角的向量求法求解.
(1)证明:![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)![]() 四边形
四边形![]() 和
和![]() 都是边长为2的正方形,
都是边长为2的正方形,
![]() ,
,![]() ,
,
![]() 就是二面角
就是二面角![]() 的平面角,
的平面角,
![]() .
.
连接![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
![]() 平面
平面![]() .
.
以点![]() 为原点,
为原点,![]() ,
,![]() (
(![]() 是
是![]() 中点),
中点),![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
如图所示:
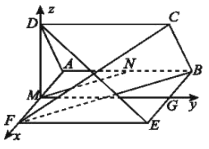
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则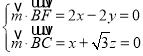 ,取
,取![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则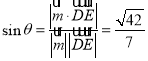 ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量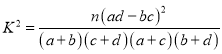 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |