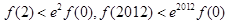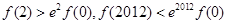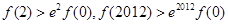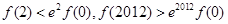题目内容
曲线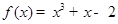 在
在 处的切线平行于直线
处的切线平行于直线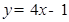 ,则
,则 的坐标为( )
的坐标为( )
| A.( 1 , 0 ) | B.( 2 , 8 ) | C.( 1 , 0 )或(-1, -4) | D.( 2 , 8 )和或(-1, -4) |
C
解析试题分析:设P0点的坐标为(a,f(a)),
由f(x)=x3+x-2,得到f′(x)=3x2+1,
由曲线在P0点处的切线平行于直线y=4x,得到切线方程的斜率为4,
即f′(a)=3a2+1=4,解得a=1或a=-1,
当a=1时,f(1)=0;当a=-1时,f(-1)=-4,
则P0点的坐标为(1,0)或(-1,-4),故选C.
考点:本题主要考查了利用导数研究曲线上某点切线方程,以及导数的几何意义,即函数在某点的导数值等于以该点为切点的切线的斜率,属于基础题.
点评:解决该试题的关键是利用导数研究曲线上某点切线方程,主要是明确两点:切点是谁,过该点的切线的斜率。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数 ,已知
,已知 在
在 时取得极值,则
时取得极值,则 =
=
| A.2 | B.3 | C.4 | D.5 |
曲线 与直线
与直线 所围成图形的面积为( )
所围成图形的面积为( )
| A.2 | B.1 | C. | D. |
已知函数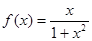 ,则
,则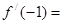
| A.-1 | B.0 | C.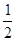 | D.1 |
已知函数 在
在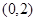 上恰有两个零点,则实数
上恰有两个零点,则实数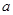 的取值范围为( )
的取值范围为( )
A.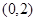 | B.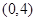 | C. | D.(2,4) |
导函数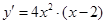 在[-2,2]上的最大值为( )
在[-2,2]上的最大值为( )
A. | B.16 | C.0 | D.5 |
曲线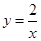 与直线
与直线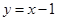 及
及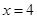 所围成的封闭图形的面积为
所围成的封闭图形的面积为
A.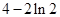 | B.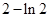 | C.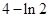 | D.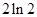 |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范
围是( )
| A.[1,+∞) | B.[1,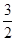 ) ) | C.[1,2) | D.[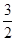 ,2) ,2) |
 是定义在R上的函数,其中
是定义在R上的函数,其中 的导函数为
的导函数为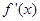 ,满足
,满足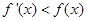 对于
对于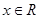 恒成立,则( )
恒成立,则( )