题目内容
已知函数 在
在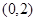 上恰有两个零点,则实数
上恰有两个零点,则实数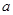 的取值范围为( )
的取值范围为( )
A.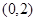 | B.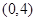 | C. | D.(2,4) |
D
解析试题分析:因为对于函数 在
在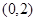 上恰有两个零点,那么可以转化为函数
上恰有两个零点,那么可以转化为函数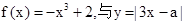 的恰有两个不同的交点,而根据三次函数的递增函数,绝对值函数的图像,与三次函数图像恰有两个公共点时,其临界值为2或者4,,数形结合思想可知结论为(2,4),选D.
的恰有两个不同的交点,而根据三次函数的递增函数,绝对值函数的图像,与三次函数图像恰有两个公共点时,其临界值为2或者4,,数形结合思想可知结论为(2,4),选D.
考点:本试题主要考查了函数的零点问题的运用。
点评:解决该试题的关键是将所求的恰有两个零点的问题,转换为函数与函数图像的交点问题来解答。即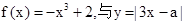 的交点来分析得到。
的交点来分析得到。

练习册系列答案
相关题目
若曲线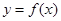 在点
在点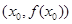 处的切线方程为
处的切线方程为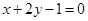 ,则
,则
A.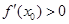 | B.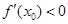 |
C.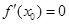 | D.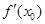 不存在 不存在 |
若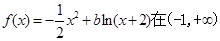 上是减函数,则
上是减函数,则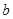 的取值范围是( )
的取值范围是( )
A.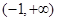 | B.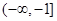 | C.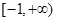 | D.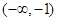 |
曲线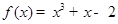 在
在 处的切线平行于直线
处的切线平行于直线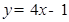 ,则
,则 的坐标为( )
的坐标为( )
| A.( 1 , 0 ) | B.( 2 , 8 ) | C.( 1 , 0 )或(-1, -4) | D.( 2 , 8 )和或(-1, -4) |
函数 有( )
有( )
| A.极大值5,极小值-27 | B.极大值5,极小值-11 |
| C.极大值5,无极小值 | D.极小值-27,无极大值 |
若函数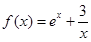 ,则此函数图像在点
,则此函数图像在点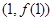 处的切线的倾斜角为( ).
处的切线的倾斜角为( ).
A.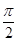 | B.0 | C.锐角 | D.钝角 |
若a>0,b>0,且函数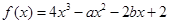 在x=1处有极值,则ab的最大值等于( )
在x=1处有极值,则ab的最大值等于( )
| A.2 | B.9 | C.6 | D.3 |
设函数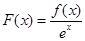 是定义在R上的函数,其中
是定义在R上的函数,其中 的导函数为
的导函数为 ,满足
,满足 对于
对于 恒成立,则( )
恒成立,则( )
A.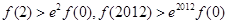 |
B.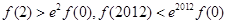 |
C.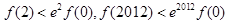 |
D.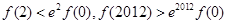 |
 是函数
是函数 的导函数,将
的导函数,将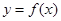 和
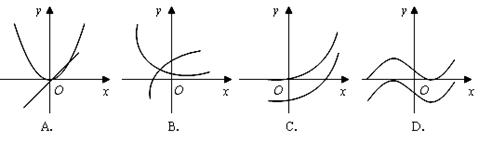
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )