Question

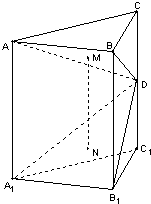如图，直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，BC=AC=2，AA₁=4，D为棱CC₁上的一动点，M、N分别为△ABD，△A₁B₁D的重心．
（1）求证：MN⊥BC；
（2）若二面角C-AB-D的大小为arctan

2

，求点C₁到平面A₁B₁D的距离；
（3）若点C在△ABD上的射影正好为M，试判断点C₁在△A₁B₁D的射影是否为N？并说明理由．

Answer 1

分析：（1）建立坐标系分别写出两条直线所在的向量，利用向量的数量积等于0可得两个向量垂直，进而得到两条直线相互垂直．
（2）求出两个平面的法向量，利用向量之间的基本运算求出二面角的平面角的余弦值，进而得到一个关于a的等式求出a的数值，再求出平面的一条斜线所在的向量在法向量上的射影即可得到点到平面的距离．
（3）因为点C在△ABD上的射影正好为M，所以

CM

⊥

AD

?

CM

•

AD

=0进而求出a的数值，再根据对称性得到C₁在平面A₁B₁D的射影正好为N．

解答：解：（1）以C₁为原点，如图建立空间直角坐标系．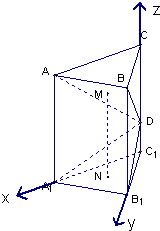
设C₁D=a（0≤a≤4），依题意有：D（0，0，a），A（2，0，4），B（0，2，4），
C（0，0，4），C₁（0，0，0）
因为M、N分别为△ABD，△A₁B₁D的重心．
所以M(

2

3

，

2

3

，

8+a

3

)，N(

2

3

，

2

3

，

a

3

)?

NM

=(0，0，

8

3

)
∵

NM

•

CB

=(0，0，

8

3

)•(0，1，0)=0
∴MN⊥BC
（2）因为平面ABC的法向量

n1

=(0，0，-1)，设平面ABD的法向量

n2

=(x1，y1，z1)
则有

AD • n2 =0 AB • n2 =0

?

(-2，0，a-4)•(x1，y1，z1)=0 (-2，2，0)•(x1，y1，z1)=0

?

n2

=(x1，x2，

2

4-a

x1)
令x1=1?

n2

=(1，1，

2

4-a

)，
设二面角C-AB-D为θ，则有tanθ=

2

?cosθ=

3

3

因此 cosθ=|

n1 • n2

| n1 |•| n2 |

|=|

2 a-4

2+( 2 4-a )2

|=|

2

2a2-16a+36

|=

3

3

?a=2
设平面A₁B₁D的法向量为

n3

=(x，y，z)，
则

A1D • n3 =0 A1B1 • n3 =0

?

(-2，0，2)•(x，y，z)=0 (-2，2，0)•(x，y，z)=0

?

n3

=(x，x，x)令x=1有

n3

=(1，1，1)
设C₁到平面A₁B₁D的距离为d，则d=

C1D • n3

| n3 |

=

2 3

3

（3）若点C在平面ABD上的射影正好为M，则

CM

⊥

AD

?

CM

•

AD

=0
即(

2

3

，

2

3

，

a-4

3

)•(-2，0，a-4)=0?

(a-4)2

3

=

4

3

?a=2，a=6（舍）
因为D为CC₁的中点，所以根据对称性可知C₁在平面A₁B₁D的射影正好为N．

点评：解决此类问题的关键是熟练掌握几何体的结构特征，进而建立空间直角坐标系以便利用空间向量解决线面的垂直关系、平行关系、空间角、空间建立等问题．