题目内容
一项体育比赛按两轮排定名次,每轮由A、B两种难度系数的4个动作构成.某选手参赛方案如表所示:
若这个选手一次正确完成难度系数为A、B动作的概率分别为0.8和0.5
(1)求这个选手在第一轮中恰有3个动作正确完成的概率;
(2)求这个选手在第二轮中两种难度系数的动作各至少正确完成一个概率.
| 动作 难度 轮次 | 1 | 2 | 3 | 4 |
| 一 | A | A | A | B |
| 二 | A | A | B | B |
(1)求这个选手在第一轮中恰有3个动作正确完成的概率;
(2)求这个选手在第二轮中两种难度系数的动作各至少正确完成一个概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)他可能前3个动作正确完成第4个动作未正确完成,也可能前3个动作恰有2个正确完成第4个也正确完成,分别求出这2件事的概率,相加即得所求.
(2)把第一种动作至少完成一个的概率,乘以第二种动作至少完成一个的概率,即为所求.
(2)把第一种动作至少完成一个的概率,乘以第二种动作至少完成一个的概率,即为所求.
解答:
解:(1)设这个选手在第一轮中恰有3个动作正确完成的事件为A,他可能前3个动作正确完成第4个动作未正确完成,
也可能前3个动作恰有2个正确完成第4个也正确完成,
所以P(A)=0.83×(1-0.5)+
×0.82×0.2×0.5=0.448.
(2)设选手在第二轮中两种难度系数的动作各至少正确完成一个的概率为事件B
则P(B)=(1-0.22)(1-0.52)=0.72.
也可能前3个动作恰有2个正确完成第4个也正确完成,
所以P(A)=0.83×(1-0.5)+
| C | 2 3 |
(2)设选手在第二轮中两种难度系数的动作各至少正确完成一个的概率为事件B
则P(B)=(1-0.22)(1-0.52)=0.72.
点评:本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
已知△ABC中,
+
=
,则D点位于( )
| ||
|
|
| ||
|
|
| AD |
| A、BC边的中线上 |
| B、BC边的高线上 |
| C、BC边的中垂线上 |
| D、∠BAC的平分线上 |
如下图①对应于函数f(x),则在下列给出的四个函数中,图②对应的函数只能是( )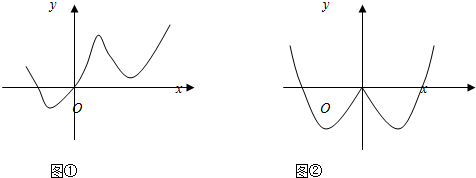

| A、y=f(|x|) |
| B、y=|f(x)| |
| C、y=f(-|x|) |
| D、y=-f(|x|) |
三角形ABC所在平面内一点P满足
•
=
•
=
•
,那么P是三角形ABC的( )
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| A、重心 | B、垂心 | C、外心 | D、内心 |
函数y=lg(
-1)的图象关于( )
| 6 |
| x+3 |
| A、原点对称 | B、x轴对称 |
| C、y轴对称 | D、直线y=x对称 |
函数f(x)=|2x-1|,若a<b<c且f(a)>f(c)>f(b),则下列四个式子是成立的是( )
| A、a<0,b<0,c<0 |
| B、a<0,b≥0,c>0 |
| C、2c+2a<2 |
| D、2-a<2c |