题目内容
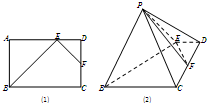 如图,E是矩形ABCD中AD边上的点,F为CD边的中点,AB=AE=
如图,E是矩形ABCD中AD边上的点,F为CD边的中点,AB=AE=| 2 | 3 |
(1)求证:平面PBE⊥平面PEF;
(2)求四棱锥P-BEFC的体积.
分析:(1)利用折叠前的图形可判断BE⊥EF,由面面垂直的性质可得EF⊥平面PBE,再由线面垂直得面面垂直;
(2)取BE的中点O,连接OP,可证PO为棱锥的高,求出棱锥的底面四边形BCFE的面积与高PO,代入公式计算.
(2)取BE的中点O,连接OP,可证PO为棱锥的高,求出棱锥的底面四边形BCFE的面积与高PO,代入公式计算.
解答:解:(1)证明:∵AB=AE=
AD=4,
∴DE=
AD=
AB=2,
∵F为CD边的中点,
∴DE=DF,又DE⊥DF,
∴∠DEF=45°,
同理∠AEB=45°,
∴∠BEF=45°,即EF⊥BE,
又平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,
∴EF⊥平面PBE,
EF?平面PEF,
∴平面PBE⊥平面PEF;
(2)取BE的中点O,连接OP,
∵PB=PE,∴PO⊥BE,
又平面PBE⊥平面BCDE,平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
即PO为棱锥P-BEFC的高,PO=2
SBEFC=SABCD-SABE-SDEF=6×4-
×4×4-
×2×2=14,
则V=
•SBEFC•h=
×14×2
=
.
| 2 |
| 3 |
∴DE=
| 1 |
| 3 |
| 1 |
| 2 |
∵F为CD边的中点,
∴DE=DF,又DE⊥DF,
∴∠DEF=45°,
同理∠AEB=45°,
∴∠BEF=45°,即EF⊥BE,
又平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,
∴EF⊥平面PBE,
EF?平面PEF,
∴平面PBE⊥平面PEF;
(2)取BE的中点O,连接OP,
∵PB=PE,∴PO⊥BE,
又平面PBE⊥平面BCDE,平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
即PO为棱锥P-BEFC的高,PO=2
| 2 |
SBEFC=SABCD-SABE-SDEF=6×4-
| 1 |
| 2 |
| 1 |
| 2 |
则V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
28
| ||
| 3 |
点评:本题利用折叠问题考查了面面垂直的证明,考查了棱锥的体积计算,解答折叠性问题要利用好折叠前图形的性质与数量关系.

练习册系列答案
相关题目
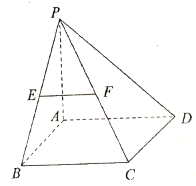 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.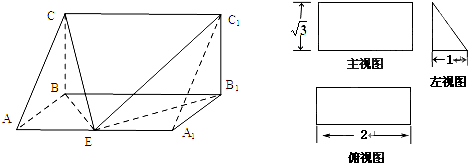

 BC,FO
BC,FO

 ,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为 ,
,