题目内容
【题目】已知![]() 过点
过点![]() ,且与
,且与![]() 内切,设
内切,设![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() ,
,
(1)求轨迹C的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,判断直线
,判断直线![]() 是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 过定点
过定点![]() .
.
【解析】
(1)由题意结合圆的性质可得![]() ,利用椭圆的定义即可得解;
,利用椭圆的定义即可得解;
(2)当直线![]() 斜率不存在时,求出各点坐标后即可得
斜率不存在时,求出各点坐标后即可得![]() 与
与![]() 轴的交点为
轴的交点为![]() ;当
;当![]() 的斜率存在时,设l的方程为
的斜率存在时,设l的方程为![]() ,联立方程可得
,联立方程可得![]() ,
,![]() ,进而可转化条件
,进而可转化条件![]() ,得出
,得出![]() 后即可得解.
后即可得解.
(1)由题意![]() 过点
过点![]() ,且与
,且与![]() 内切,
内切,
易知点![]() ,
,![]() 半径为
半径为![]() ,
,
设两圆切点为![]() ,
,
所以![]() ,在
,在![]() 中,
中,![]() ,
,
所以![]() ,所以M的轨迹为椭圆,由椭圆定义可知
,所以M的轨迹为椭圆,由椭圆定义可知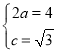 ,
,
所以![]() ,所以轨迹C的方程为
,所以轨迹C的方程为![]() ;
;
(2)①当![]() 的斜率不存在的时,设
的斜率不存在的时,设![]() ,所以
,所以![]() ,
,
所以 ,解得
,解得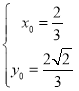 或
或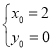 (舍),
(舍),
所以![]() 与
与![]() 轴的交点为
轴的交点为![]() ;
;
②当![]() 的斜率存在时,设l的方程为
的斜率存在时,设l的方程为![]() ,
,
联立 消元可得
消元可得![]() ,
,
![]() ,所以
,所以![]() ,
,
由韦达定理![]() ,
,![]() ,
,
则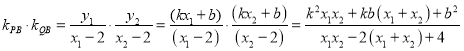
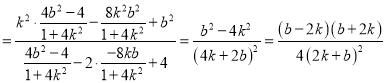 ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以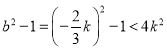 ,所以
,所以![]() 成立,
成立,
所以![]() ,当
,当![]() 时,
时,![]() ,所以l过
,所以l过![]() ,
,
综上所述,![]() 过定点
过定点![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数![]() 浓度,制定了空气质量标准:
浓度,制定了空气质量标准:
空气污染质量 |
|
|
|
|
|
|
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
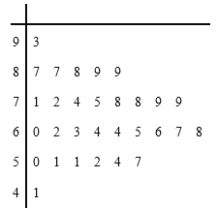
某市政府为了打造美丽城市,节能减排,从2010年开始考查了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号为字母的,前13个视为单号,后13个视为双号).
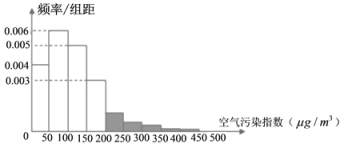
(1)某人计划11月份开车出行,求因空气污染被限号出行的概率;
(2)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行三年来的11月份共90天的空气质量进行统计,其结果如表:
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 16 | 39 | 18 | 10 | 5 | 2 |
根据限行前六年180天与限行后90天的数据,计算并填写![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为空气质量的优良与汽车尾气的排放有关.
的把握认为空气质量的优良与汽车尾气的排放有关.
空气质量优良 | 空气质量污染 | 合计 | |
限行前 | |||
限行后 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()