题目内容
若sin( -α)=-
-α)=-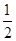 ,sin(
,sin( +β)=
+β)= ,其中
,其中 <α<
<α< ,
, <β<
<β< ,求 角(α+β)的值.
,求 角(α+β)的值.
α+β=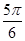 。
。
解析试题分析:先由 <α<
<α< ,
, <β<
<β< 可知-
可知- <
< -α<0,
-α<0, <
< +β<
+β<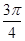 ,
,
从而可由sin( -α),sin(
-α),sin( +β)求出cos(
+β)求出cos( -α),cos(
-α),cos( +β),
+β),
然后再利用cos(α+β)=cos[( +β)-(
+β)-( -α)]=cos(
-α)]=cos( +β)·cos(
+β)·cos( -α)+sin(
-α)+sin( +β)·sin(
+β)·sin( -α)代入求值,再根据
-α)代入求值,再根据 <α+β<π,从而确定α+β的值.
<α+β<π,从而确定α+β的值.
∵ <α<
<α< ,-
,- <
< -α<0,
-α<0, <β<
<β< ,
, <
< +β<
+β<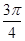 (3分)
(3分)
由已知可得cos( -α)=
-α)=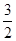 ,cos(
,cos( +β)=-
+β)=-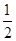
则cos(α+β)=cos[( +β)-(
+β)-( -α)]=cos(
-α)]=cos( +β)·cos(
+β)·cos( -α)+sin(
-α)+sin( +β)·sin(
+β)·sin( -α)=-
-α)=-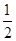 ×
×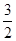 +
+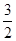 ×(-
×(-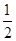 )=-
)=-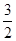 ,…………(9分)
,…………(9分)
∵ <α+β<π ∴α+β=
<α+β<π ∴α+β=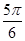 …………(12分).
…………(12分).
考点:给值求角,两角差的余弦公式.
点评:解本小题首先要利用同角的三角函数的平方关系求出余角的值,一定要把角的范围搞清楚,然后再注意利用α+β=( +β)-(
+β)-( -α)把未知角用已知角表示出来,借助两角差的余弦公式求解即可.
-α)把未知角用已知角表示出来,借助两角差的余弦公式求解即可.

练习册系列答案
相关题目
 ,其中
,其中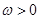 .
. ,求函数f(x)的最小正周期;
,求函数f(x)的最小正周期; 满足
满足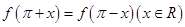 ,且
,且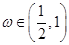 ,求函数f(x)的单调递减区间.
,求函数f(x)的单调递减区间.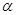 是第三角限角,化简
是第三角限角,化简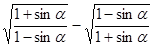 .
. 已知函数
已知函数 ,
, .
.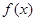 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 上的最小值和最大值,并求出取得最值时
上的最小值和最大值,并求出取得最值时 的值.
的值.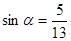 ,求
,求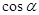 ,
,
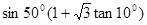 ,
,  ,求sin
,求sin 的值。
的值。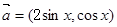 ,
,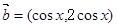 ,函数
,函数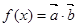 .
. 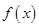 的最小正周期和最大值;
的最小正周期和最大值;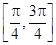 上的最大值和最小值.
上的最大值和最小值. 
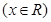 的图象经过点
的图象经过点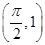 .
.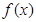 的解析式,并求函数的最小正周期.
的解析式,并求函数的最小正周期. 且
且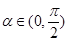 ,求
,求 的值。
的值。 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;  一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的?