题目内容
(2011•枣庄二模)已知函数y=
是偶函数,f(x)=logax的图象过点(2,1),则y=g(x)对应的图象大致是( )
|
分析:由f(x)=logax的图象过点(2,1)可求a,进而可求f(x),然后根据函数y=
是偶函数,函数的图象关于y轴对称可求g(x)的解析式,进而可判断函数的图象
|
解答:解:∵f(x)=logax的图象过点(2,1)
∴f(2)=loga2=1
∴a=2,f(x)=log2x
∵函数y=
是偶函数,函数的图象关于y轴对称
∴g(x)=f(-x)=log2(-x)(x<0),
故选B
∴f(2)=loga2=1
∴a=2,f(x)=log2x
∵函数y=
|
∴g(x)=f(-x)=log2(-x)(x<0),
故选B
点评:本题主要考查了对数函数的图象的变换,偶函数的图象关于y轴对称的性质的应用,属于中档 试题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
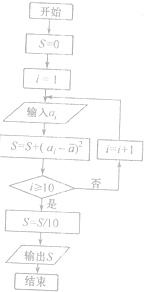 (2011•枣庄二模)某地某一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物,第i天监测得到的数据记为ai,
(2011•枣庄二模)某地某一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物,第i天监测得到的数据记为ai,