题目内容
(2011•枣庄二模)已知函数f(x)=
sin2x-
(cos2x-sin2x)-1,x∈R
(1)求函数f(x)的最小值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,若c=
,f(C)=0,sinB=3sinA,求a,b的值.
| ||
| 2 |
| 1 |
| 2 |
(1)求函数f(x)的最小值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,若c=
| 7 |
分析:(1)利用二倍角公式以及两角差的正弦函数化简函数的表达式,借助正弦函数的有界性,求出函数的最小值.
(2)通过f(C)=2,利用三角形的内角,求出C的值,通过余弦定理,正弦定理求出a,b的值即可.
(2)通过f(C)=2,利用三角形的内角,求出C的值,通过余弦定理,正弦定理求出a,b的值即可.
解答:解:(1)函数f(x)=
sin2x-
(cos2x-sin2x)-1=sin(2x-
)-1,
显然,函数的最小值为-2.
(2)由f(C)=0,可得sin(2C-
)-1=0,因为C是三角形内角,所以2C-
=
,即C=
,
由余弦定理a2+b2-2abcos
=(
)2…①
又sinB=3sinA,所以b=3a…②
解①②得a=1,b=3.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
显然,函数的最小值为-2.
(2)由f(C)=0,可得sin(2C-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
由余弦定理a2+b2-2abcos
| π |
| 3 |
| 7 |
又sinB=3sinA,所以b=3a…②
解①②得a=1,b=3.
点评:本题是中档题,考查三角函数的化简求值,正弦定理、余弦定理的应用,考查计算能力常考题型.注意三角形内角的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
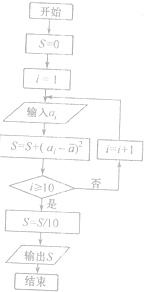 (2011•枣庄二模)某地某一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物,第i天监测得到的数据记为ai,
(2011•枣庄二模)某地某一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物,第i天监测得到的数据记为ai,