题目内容
定义在（-1，1）上的函数f（x）=-5x+sinx，如果f（1-a）+f（1-a2）＞0，则实数a的取值范围为________．
（1，
）
分析：函数f（x）=-5x+sinx且定义域为（-1，1），可判断此函数为奇函数，且在定义域内为单调递减函数，所以f（1-a）+f（1-a2）＞0?f（1-a）＞-f（1-a2），然后进行求解即可．
解答：∵f（x）=-5x+sinx，
∴f（-x）=5x-sinx=-（-5x+sinx）=-f（x），又x∈（-1，1）
∴f（x）为奇函数；
∴f（1-a）+f（1-a2）＞0?f（1-a）＞-f（1-a2）=f（a2-1），
又f′（x）=-5+cosx＜0，
∴f（x）为减函数；
∴-1＜1-a＜a2-1＜1，
解得：
．
故答案为：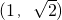
．
点评：此题考查了利用函数的单调性及奇偶性求解抽象函数的不等式，还考查了不等式的求解及集合的交集．
）分析：函数f（x）=-5x+sinx且定义域为（-1，1），可判断此函数为奇函数，且在定义域内为单调递减函数，所以f（1-a）+f（1-a2）＞0?f（1-a）＞-f（1-a2），然后进行求解即可．
解答：∵f（x）=-5x+sinx，
∴f（-x）=5x-sinx=-（-5x+sinx）=-f（x），又x∈（-1，1）
∴f（x）为奇函数；
∴f（1-a）+f（1-a2）＞0?f（1-a）＞-f（1-a2）=f（a2-1），
又f′（x）=-5+cosx＜0，
∴f（x）为减函数；
∴-1＜1-a＜a2-1＜1，
解得：
．故答案为：
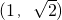．点评：此题考查了利用函数的单调性及奇偶性求解抽象函数的不等式，还考查了不等式的求解及集合的交集．
练习册系列答案
阅读快车系列答案
相关题目
＞0.
)＜f(
).
是定义在（-1，1）的奇函数，且f（
）=
．
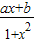是定义在（-1，1）的奇函数，且f（
）=
．