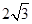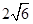题目内容
设正实数x,y,z满足x2-3xy+4y2-z=0,则当 取得最大值时,x+2y-z的最大值为( )
取得最大值时,x+2y-z的最大值为( )
 取得最大值时,x+2y-z的最大值为( )
取得最大值时,x+2y-z的最大值为( )| A.0 | B. | C.2 | D. |
C
由题得z+3xy=x2+4y2≥4xy(x,y,z>0),
即z≥xy, ≥1.当且仅当x=2y时等号成立,
≥1.当且仅当x=2y时等号成立,
则x+2y-z=2y+2y-(4y2-6y2+4y2)
=4y-2y2=-2(y2-2y)
=-2[(y-1)2-1]=-2(y-1)2+2.
当y=1时,x+2y-z有最大值2.故选C.
即z≥xy,
 ≥1.当且仅当x=2y时等号成立,
≥1.当且仅当x=2y时等号成立,则x+2y-z=2y+2y-(4y2-6y2+4y2)
=4y-2y2=-2(y2-2y)
=-2[(y-1)2-1]=-2(y-1)2+2.
当y=1时,x+2y-z有最大值2.故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
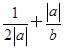 取得最小值.
取得最小值.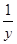 ,b=y+
,b=y+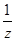 ,c=z+
,c=z+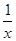 ,则a,b,c三数( )
,则a,b,c三数( )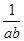 的最小值为( )
的最小值为( )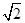
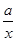 (x>0,a>0)在x=3时取得最小值,则a= .
(x>0,a>0)在x=3时取得最小值,则a= . ,
,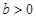 ,若
,若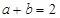 ,则
,则 的最小值为
的最小值为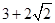
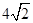
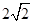
 的函数
的函数 的图象的两个端点为
的图象的两个端点为 ,
, 是
是 图象上任意一点,其中
图象上任意一点,其中 ,向量
,向量 ,若不等式
,若不等式 恒成立,则称函数
恒成立,则称函数 阶线性近似”. 若函数
阶线性近似”. 若函数 上“
上“



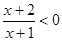 的解集为
的解集为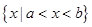 ,点
,点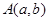 在直线
在直线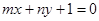 上,其中
上,其中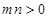 ,则
,则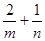 的最小值为( )
的最小值为( )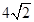
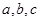 满足
满足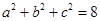 ,则
,则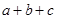 的最大值为( )
的最大值为( )