题目内容
【题目】已知函数f(x)=2x3﹣3ax2+1.
(1)若a=﹣1,求函数f(x)的单调区间;
(2)若函数f(x)有且只有2个不同的零点,求实数a的值;
(3)若函数y=|f(x)|在[0,1]上的最小值是0,求实数a的取值范围.
【答案】(1)函数f(x)的增区间为(﹣∞,﹣1),(0,+∞),减区间为(﹣1,0)
(2)1
(3)[1,+∞)
【解析】
(1)求出![]() 的导数,解关于导函数的不等式,求出函数的单调区间即可;
的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)通过讨论![]() 的范围,确定函数的单调性, 函数
的范围,确定函数的单调性, 函数![]() 有且只有
有且只有![]() 个不同的零点即可求得
个不同的零点即可求得![]() 的值;
的值;
(3)通过讨论![]() 的范围,确定函数的单调性,再根据函数
的范围,确定函数的单调性,再根据函数![]() 在
在![]() 上的最小值是
上的最小值是![]() 并结合图像可求得实数
并结合图像可求得实数![]() 的取值范围.
的取值范围.
(1)![]() 时,
时,![]() .
.
![]() 当
当![]() ,
,![]() 时,
时,
![]() ,
,
当![]() 时,
时,![]() ,
,
故函数![]() 的增区间为
的增区间为![]() ,
,![]() ,减区间为
,减区间为![]() .
.
(2)![]() ,
,![]()
①![]() 时,
时,![]() 在
在![]() 上单调递增,不存在两个零点;
上单调递增,不存在两个零点;
②![]() 时,
时,![]() 在
在![]() ,
,![]() 递增,在
递增,在![]() 递减.
递减.
其图象如下:
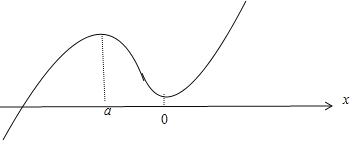
函数![]() 不存在2个不同的零点;
不存在2个不同的零点;
③![]() 时,
时,![]() 在
在![]() ,
,![]() 递增,在
递增,在![]() 递减.
递减.
其图象如下:
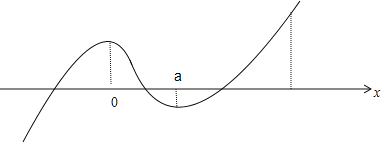
![]() 只需
只需![]() ,
,![]() 即可
即可
综上,函数![]() 有且只有
有且只有![]() 个不同的零点,实数
个不同的零点,实数![]() 的值为
的值为![]() .
.
(3)①![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,不符合题意;
,不符合题意;
②![]() 时,
时,![]() 在
在![]() 递增,
递增,![]() ,不符合题意;
,不符合题意;
③![]() 时,
时,![]() 在
在![]() ,
,![]() 递增,在
递增,在![]() 递减.
递减.
![]() 图象如下:
图象如下:

要使函数![]() 在
在![]() 上的最小值是
上的最小值是![]() ,只需
,只需![]() ,
,![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
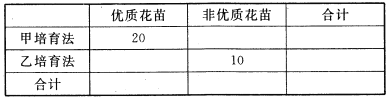
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
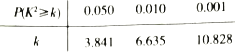 .
.