题目内容
某市有210名初中学生参加数学竞赛预赛，随机调阅了60名学生的答卷，成绩列表如下：
（1）求样本的数学平均成绩及标准差；（精确到0.01）
（2）若总体服从正态分布，求此正态曲线的近似方程.
| 成绩（分） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数分布 | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
（2）若总体服从正态分布，求此正态曲线的近似方程.
（1）样本的数学平均成绩为6分，标准差约为1.22（2）正态曲线的近似方程为
P（x）=
.
P（x）=
. （1）平均成绩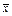
=
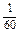（4×6+5×15+6×21+7×12+8×3+9×3）=6.
s2=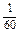［6×(4-6)2+15×(5-6)2+21×(6-6)2+12×(7-6)2+3×(8-6)2+3×(9-6)2］=1.5.
∴s≈1.22,
即样本的数学平均成绩为6分，标准差约为1.22.
（2）以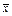=6，s=1.22作为总体学生的数学平均成绩和标准差的估计值.
即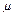
=6,
=1.22.
则总体服从正态分布N（6，1.222）.
正态曲线的近似方程为
P（x）=.
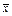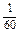=（4×6+5×15+6×21+7×12+8×3+9×3）=6.s2=
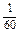［6×(4-6)2+15×(5-6)2+21×(6-6)2+12×(7-6)2+3×(8-6)2+3×(9-6)2］=1.5.∴s≈1.22,
即样本的数学平均成绩为6分，标准差约为1.22.
（2）以
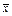=6，s=1.22作为总体学生的数学平均成绩和标准差的估计值.即
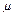=6,=1.22.则总体服从正态分布N（6，1.222）.
正态曲线的近似方程为
P（x）=
.
练习册系列答案
相关题目
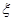服从标准正态分布N（0,1），已知
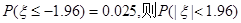等于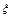
服从一个正态分布，即
,
,则
= .
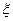服从正态分布
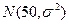，若
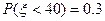，则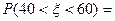
.